2015-04-01
332
К логарифмическим уравнения относятся уравнения, содержащие неизвестное под знаком логарифма или в основании логарифма.
Простейшее логарифмическое уравнение вида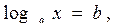 
где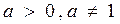 
имеет решение 
.
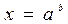Аналогично решается уравнение вида
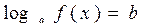, где 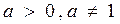, эквивалентно системе
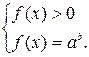
Уравнение вида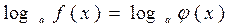 
, где 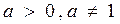методом потенцирования приводится к равносильной системе
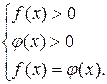
Этот метод лежит в основе решения многих логарифмических уравнений, приводимых к виду равенства логарифмов.
Простейшее уравнение вида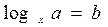 
, где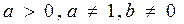 
приводится к равносильному уравнению 
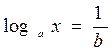с множеством допустимых значений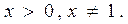 
При решении уравнений второй и выше степени относительно логарифма необходимо обратить внимании на следующие преобразования:
1. 
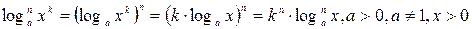
2. 
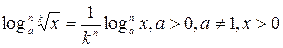
3. 
.
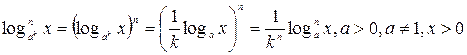Уравнения второй и более высоких степеней относительно логарифма решаются по методу замены переменной, а именно полагают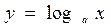 
. В результате замены переменной получается рациональное (или иррациональное) уравнение относительно у, корни которого подставляют в простейшее логарифмическое уравнение 
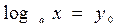, где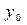 
- рассматриваемый корень.
Решение логарифмических неравенств основано на том, что функция 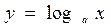при 
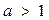монотонно возрастает, а при 
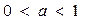монотонно убывает.
С помощью методов, аналогичных методам решения логарифмических уравнений, логарифмическое неравенство сводится к простейшему виду:
1. 
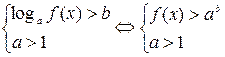
2. 
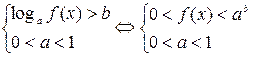
3. 
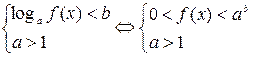
4. 
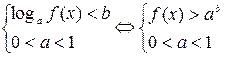
5. 
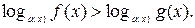Это неравенство эквивалентно совокупности двух систем неравенств:
.
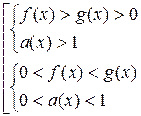Множество решений нестрогого неравенства находится как объединение множеств решений соответствующего строгого неравенства и соответствующего уравнения.
