Пример 1. Решите уравнение: 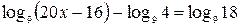 .
.
Решение. Воспользуемся свойством логарифма и левую часть приведем к одному основанию
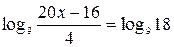 ,
,
полученное уравнение равносильно системе
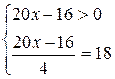
Ответ. 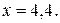
Пример 2. Какому промежутку принадлежат корни уравнения 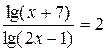 .
.
Решение. Приведем к общему знаменателю
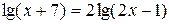
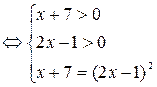
Корни уравнения системы х=2 и 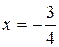 , но корень
, но корень 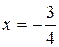 не удовлетворяет второму неравенству системы.
не удовлетворяет второму неравенству системы.
Ответ. 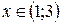 .
.
Пример 3. Решить уравнение
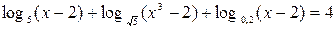
Укажем, что x >2 (ОДЗ). Далее, сводим все логарифмы к единому основанию 5:
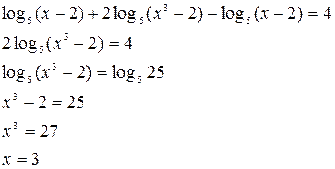
Ответ подходит под ОДЗ.
Ответ. 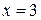 .
.
Пример 4. Решить уравнение 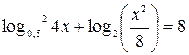
Решение. Укажем, что x > 0.
Так как 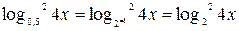 и, используя свойства логарифма, имеем:
и, используя свойства логарифма, имеем:
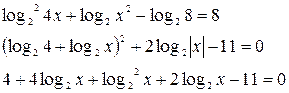
Сделаем замену 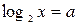 , тогда
, тогда
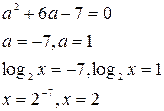
Ответ. 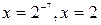
Пример 5. Решить неравенство 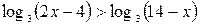 .
.
Решение.
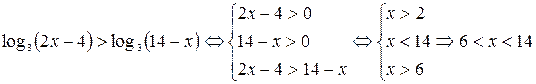
Ответ. 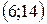 .
.
Пример 6. Решить неравенство 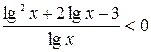 .
.
Решение. Введём новую переменную 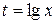
Решив полученное неравенство методом интервалов, получим 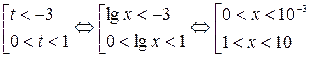
Ответ. 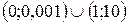 .
.
Пример 7. Решить неравенство 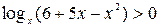
Решение. Это неравенство равносильно совокупности двух неравенств:
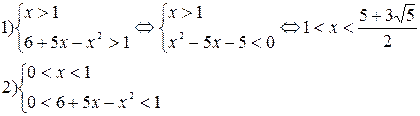
Вторая система не имеет решения.
Ответ: 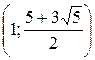 .
.
 2015-04-01
2015-04-01 312
312








