Пример 1. Доказать тождество 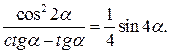
Доказательство. Преобразуем левую часть тождества:
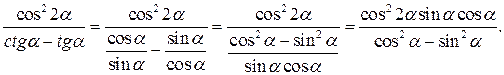
По формулам 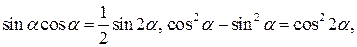
Поэтому 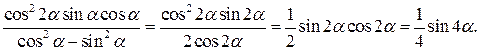
Итак, тождество доказано. При этом 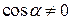 и
и 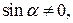 т.е.
т.е. 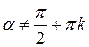 и
и 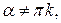 а, значит,
а, значит, 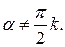
Кроме того, 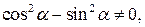 т.е.
т.е. 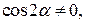 откуда
откуда 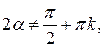 или
или 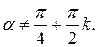
Таким образом, приходим к выводу, что тождество выполняется при 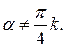
Пример 2. Доказать тождество 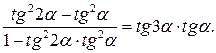
Решение. Разложим на множители числитель и знаменатель выражения, содержащегося в левой части тождества:
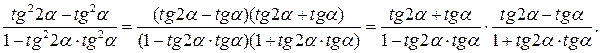
Далее используя формулу 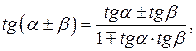 получаем:
получаем:
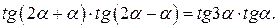
Доказанное тождество выполняется при 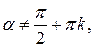
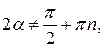
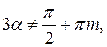 т.е. при
т.е. при 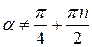 и
и 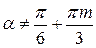 (множество
(множество  всех чисел вида
всех чисел вида 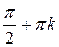 содержится в множестве
содержится в множестве 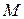 всех чисел вида
всех чисел вида 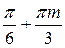 ).
).
Пример 3. Упростить выражение 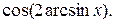
Решение. 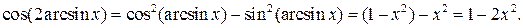
Пример 4. Вычислить 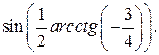
Решение. Пусть 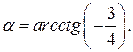 Тогда
Тогда 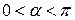 и
и 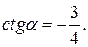 Более того, так как
Более того, так как 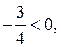 то
то 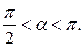 Для вычисления
Для вычисления 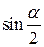 воспользуемся формулой
воспользуемся формулой 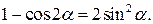 Из нее следует, что
Из нее следует, что 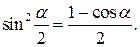 Таким образом, необходимо сначала найти
Таким образом, необходимо сначала найти 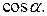 Так как
Так как 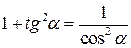 и ясно, что
и ясно, что 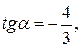 то
то 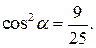
Так как в интервале 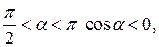 то
то 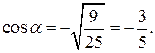 Итак
Итак 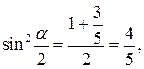 и так как
и так как 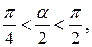 а в этом интервале синус принимает только положительные значения, то
а в этом интервале синус принимает только положительные значения, то 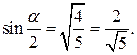 Таким образом
Таким образом 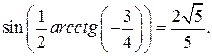
Пример 5. Вычислить 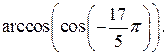
Решение. Положим 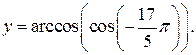 Тогда
Тогда 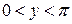 и
и 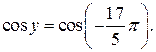 Но
Но 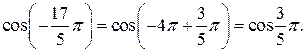 Таким образом,
Таким образом, 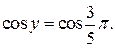 Итак
Итак 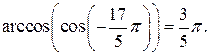
Замечание. Ясно, что равенство 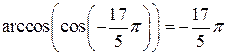 ложно.
ложно.
Действительно, по определению значения косинуса принадлежат отрезку 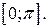 Значение же
Значение же 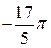 этому отрезку не принадлежит.
этому отрезку не принадлежит.
 2015-04-01
2015-04-01 1116
1116
