Краткие теоретические сведения. Скалярным произведением двух векторов (обозначается 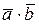или ) называется число, равное произведению длин этих векторов на косинус угла между ними

Скалярным произведением двух векторов (обозначается или 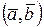) называется число, равное произведению длин этих векторов на косинус угла между ними: 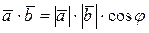, где .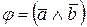

Свойства скалярного произведения:

1) ;

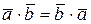2) ;

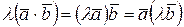3) ;

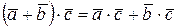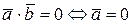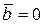4) , или , или .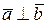

Таким образом, 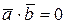– условие перпендикулярности векторов.

5) 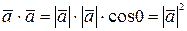, или, обозначая 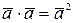(скалярный квадрат вектора 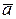), получим 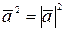, откуда .

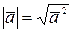Если вектор 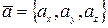, а вектор 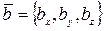, то скалярное произведение этих векторов находится по формуле: .

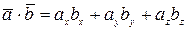Векторным произведением двух векторов называется вектор, который обозначается 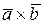или 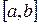и определяется следующим образом:

1) 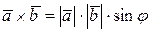где 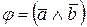– длина этого вектора равна произведению длин перемножаемых векторов на синус угла между ними;

2) ` 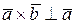, 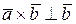этот вектор перпендикулярен каждому из перемножаемых векторов;

3) Векторы 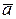, , 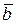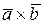образуют правую тройку.

Из условия (1) следует, что модуль вектора 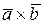численно равен площади параллелограмма, построенного на векторах 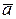и 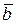как на сторонах (рис 13.1): , .

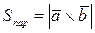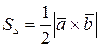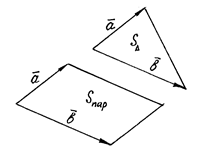
Рис. 13.1

Свойства векторного произведения:

1) ;

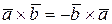2) ;

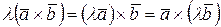3) ;

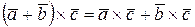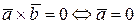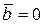4) , или , или .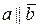

4a) .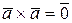

Если вектор 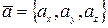, а вектор 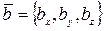, то векторное произведение этих векторов находится по формуле: .

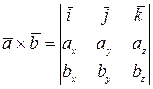Смешанным, или векторно-скалярным произведением трех векторов (обозначается 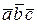) называется произведение вида .

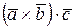Если вектор 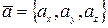, вектор 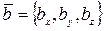, а вектор 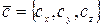то смешанное произведение этих векторов находится по формуле: .

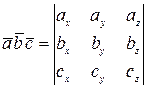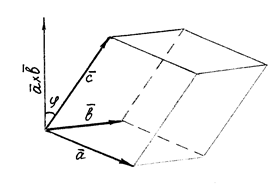
Рис. 13.2

Можно записать: .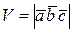

Объем тетраэдра, построенного на векторах 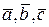равен .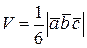

Заметим, что если векторы 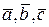образуют правую тройку, то 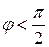и` 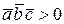, а если левую, то 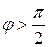и .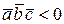

Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.