Напомним общие формулы решений простейших тригонометрических уравнений (если не сделано оговорок, то предполагается, что параметры 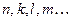 принимают целые значения).
принимают целые значения).
| Уравнение | Решение |
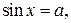 где где 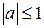
| 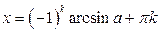
|
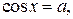 где где 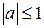
| 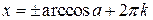
|
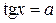
| 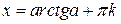
|
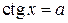
| 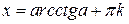
|
Отметим особо некоторые частные случаи простейших тригонометрических уравнений, когда решение может быть записано без применения общих формул:
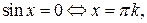
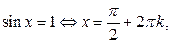
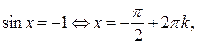
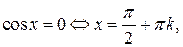
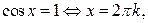
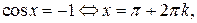
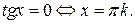
Проверка найденных решений необходима:
1) если в процессе решения произошло расширение области определения уравнения в результате некоторых преобразований (освобождение от знаменателей, сокращение дроби, приведение подобных членов),
2) если в процессе решения уравнения использовалась возведение обеих частей уравнения в одну и ту же четную степень,
3) если при решении применялись тригонометрические тождества, левая и правая части которых имеют неодинаковые определения.
Основными методами, используемыми при решении тригонометрических уравнений, являются следующие методы:
1) разложение на множители;
2) введение новых переменных.
В результате разложения на множители решение заданного уравнения сводится к решению совокупности уравнений. Это, в свою очередь, означает, что после решения всех уравнений совокупности найденные семейства (множества) решении следует объединить. Объединяя семейства решений, иногда добиваются более компактной записи ответа.
При решении уравнений методом введения новых переменных следует помнить, что важную роль играет выбор функций, через которую выражаются остальные функции.
Рассмотрим уравнение вида 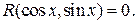 В некоторых случаях удается свести такое уравнение к рациональному уравнению относительно
В некоторых случаях удается свести такое уравнение к рациональному уравнению относительно 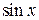 (или относительно
(или относительно 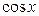 ). Укажем некоторые правила, облегчающие выбор подстановки при решении тригонометрических уравнений. Если
). Укажем некоторые правила, облегчающие выбор подстановки при решении тригонометрических уравнений. Если 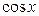 входит в уравнение лишь в четных степенях, то, заменяя всюду
входит в уравнение лишь в четных степенях, то, заменяя всюду 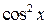 на
на 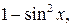 получим рациональное уравнение относительно
получим рациональное уравнение относительно 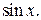 Точно так же если
Точно так же если 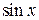 входит в уравнение лишь в четных степенях, то замена
входит в уравнение лишь в четных степенях, то замена 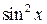 на
на 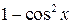 приводит уравнение к рациональному виду относительно
приводит уравнение к рациональному виду относительно 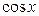 .
.
Однородным тригонометрическим уравнением первой степени называется уравнение вида 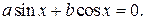
Однородным тригонометрическим уравнением второй степени называется уравнение вида 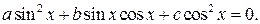
Аналогично может быть определено однородное тригонометрическое уравнение любой натуральной степени 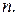
Рассмотрим случай, когда 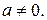 Нетрудно видеть, что при
Нетрудно видеть, что при 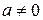 однородному уравнению не удовлетворяют те значения
однородному уравнению не удовлетворяют те значения 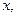 при которых
при которых 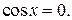 Поэтому деление на
Поэтому деление на 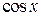 (на
(на 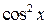 ) обеих частей однородного уравнения первой (второй) степени в случае
) обеих частей однородного уравнения первой (второй) степени в случае 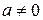 приводит к равносильному уравнению. Разделим обе части однородного уравнения первой степени на
приводит к равносильному уравнению. Разделим обе части однородного уравнения первой степени на 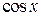 а обе части однородного уравнения второй степени на
а обе части однородного уравнения второй степени на 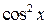 . В результате получим соответственно следующие уравнения, рациональные относительно
. В результате получим соответственно следующие уравнения, рациональные относительно 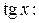
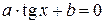 и
и 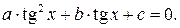
Эти уравнения решаются с помощью подстановки 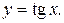
 2015-04-01
2015-04-01 643
643








