Пусть 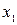 и
и 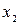 - значения аргумента, а
- значения аргумента, а 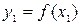 и
и 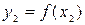 - соответствующие значения аргумента функции
- соответствующие значения аргумента функции 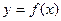 . Разность
. Разность 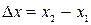 называется приращением аргумента, а разность
называется приращением аргумента, а разность 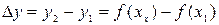 - приращением функции на отрезке
- приращением функции на отрезке 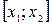 .
.
Производной от функции 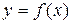 по аргументу
по аргументу 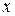 называется конечный предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
называется конечный предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
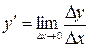 , или
, или 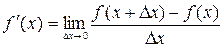 .
.
Геометрически производная представляет собой угловой коэффициент касательной к графику функции 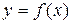 в точке
в точке 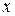 , т.е.
, т.е. 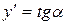 .
.
Производная есть скорость изменения функции в точке 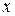 .
.
Отыскание производной называется дифференцированием функции.
Формулы дифференцирования основных функций:
1. 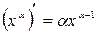 ; 2.
; 2. 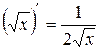 ;
;
3. 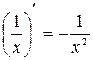 ; 4.
; 4. 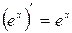 ;
;
5. 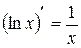 ; 6.
; 6. 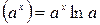 ;
;
7. 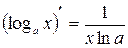 ; 8.
; 8. 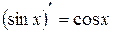 ;
;
9. 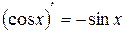 ; 10.
; 10. 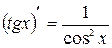 ;
;
11. 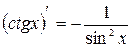 ; 12.
; 12. 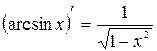 ;
;
13. 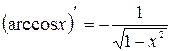 ; 14.
; 14. 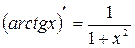 ;
;
15. 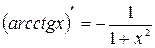 .
.
Основные правила дифференцирования:
Пусть 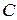 - постоянная,
- постоянная, 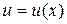 ,
, 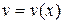 - функции, имеющие производные. Тогда:
- функции, имеющие производные. Тогда:
1. 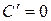 ;
;
2. 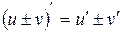 ;
;
3. 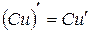 ;
;
4. 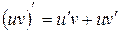 ;
;
5. 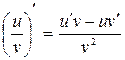 ;
;
6. если 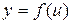 ,
, 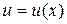 , т.е.
, т.е. 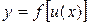 , где функции
, где функции 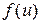 и
и 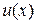 имеют производные, то
имеют производные, то 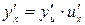 .
.
 2015-04-01
2015-04-01 444
444








