Пример 1. Вычислить предел 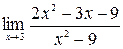 .
.
Решение. Подставив значение х=3, получаем неопределённость вида 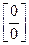 . З десь необходимо и числитель, и знаменатель разложить на множители.
. З десь необходимо и числитель, и знаменатель разложить на множители.
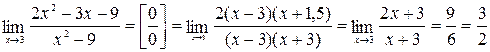 .
.
Ответ. 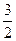 .
.
Пример 2. Вычислить предел 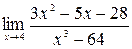 .
.
Решение. При 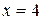 возникает неопределённость вида
возникает неопределённость вида 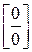 . Для раскрытия этой неопределённости разлагаем числитель и знаменатель дроби на множители. Здесь используем формулу разности кубов
. Для раскрытия этой неопределённости разлагаем числитель и знаменатель дроби на множители. Здесь используем формулу разности кубов 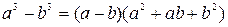
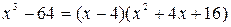 .
.
Итак, 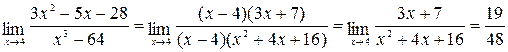
Ответ. 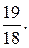
Пример 3. Вычислить предел 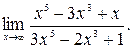
Решение. Подставим 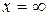 в дробь. В данном случае получена так называемая неопределенность
в дробь. В данном случае получена так называемая неопределенность 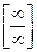 .
.
Если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 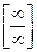 , то для ее раскрытия необходимо разделить числитель и знаменатель дроби на х в наивысшей степени. Разделим числитель и знаменатель дроби на
, то для ее раскрытия необходимо разделить числитель и знаменатель дроби на х в наивысшей степени. Разделим числитель и знаменатель дроби на 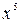 и подставим
и подставим 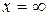 в полученное выражение:
в полученное выражение:
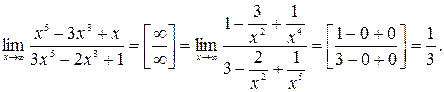
Ответ. 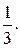
Замечание: При решении примеров этого типа могут возникнуть ситуации 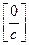 или
или 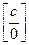 , где с=const. Здесь надо иметь в виду, что
, где с=const. Здесь надо иметь в виду, что 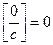 и
и 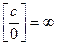 .
.
Пример 4:Вычислить предел 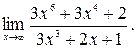
Решение: Наивысшая степень многочленов числителя и знаменателя – 6. Поделив и числитель, и знаменатель на 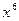 , получим:
, получим:
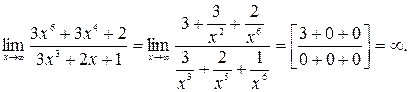
Ответ: 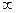 .
.
 2015-04-01
2015-04-01 408
408








