Пусть функция 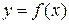 имеет производную
имеет производную 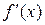 в каждой точке
в каждой точке 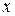 некоторого множества
некоторого множества 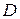 . Тогда ее производную
. Тогда ее производную 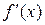 можно рассматривать как функцию, определенную на множестве
можно рассматривать как функцию, определенную на множестве 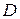 . В свою очередь функция
. В свою очередь функция 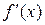 может в некоторых точках множества
может в некоторых точках множества 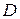 иметь производную. В этом случае производной второго порядка (второй производной) называется производная от производной
иметь производную. В этом случае производной второго порядка (второй производной) называется производная от производной 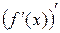 . Для второй производной функции
. Для второй производной функции 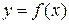 в точке
в точке 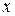 применяются обозначения:
применяются обозначения: 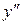 ,
, 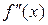 ,
, 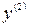 ,
, 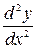 .
.
Аналогично определяются производные 3-го, 4-го и т.д. порядков. Производной первого порядка (или первой производной) считается 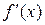 .
.
Формула Тейлора. Функция  , дифференцируемая
, дифференцируемая 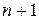 раз в некотором интервале, содержащем точку
раз в некотором интервале, содержащем точку 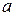 , может быть представлена в виде суммы многочлена
, может быть представлена в виде суммы многочлена 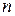 -й степени и остаточного члена
-й степени и остаточного члена 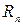 :
:
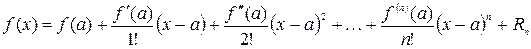 ;
;
(1)
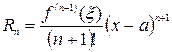 , где точка
, где точка 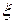 лежит между точками
лежит между точками 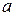 и
и 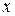 , т.е.
, т.е. 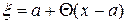 , причем
, причем 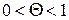 .
.
При 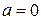 получается формула Маклорена
получается формула Маклорена
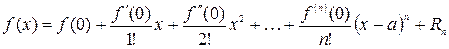 , где
, где
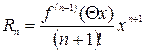 ,
, 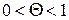 . (2)
. (2)
 2015-04-01
2015-04-01 474
474








