Исследовать на сходимость интегралы и вычислить их.
32.1. 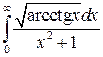 . 32.2.
. 32.2. 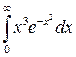 .
.
32.3. 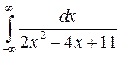 . 32.4.
. 32.4. 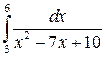 .
.
32.5. 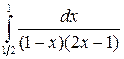 . 32.6.
. 32.6. 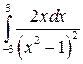 .
.
32.7. 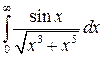 32.8.
32.8. 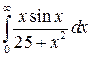 .
.
32.9. 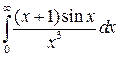 32.10.
32.10. 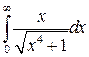 .
.
32.11. 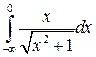 .
.
Домашнее задание
Исследовать на сходимость интегралы и вычислить их.
32.12. 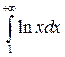 . 32.13.
. 32.13. 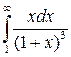 .
.
32.14. 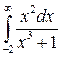 . 32.15.
. 32.15. 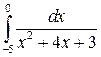 .
.
32.16. 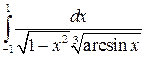 . 32.17.
. 32.17. 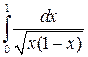 .
.
32.18. 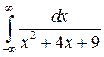 . 32.19.
. 32.19. 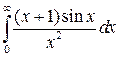 .
.
Ответы
32.1. 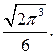 32.2.
32.2. 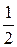 . 32.3.
. 32.3. 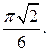 32.4.
32.4. 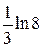 . 32.5.
. 32.5. 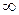 . 32.6. не существует. 32.8.
. 32.6. не существует. 32.8. 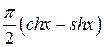 . 32.9.
. 32.9. 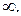 32.10.
32.10. 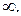 32.11.
32.11. 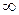 . 32.12.
. 32.12. 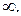 32.13.
32.13. 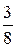 . 32.14.
. 32.14. 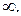 32.15.
32.15. 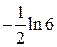 . 32.17.
. 32.17. 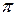 . 32.18.
. 32.18. 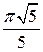 . 32.19.
. 32.19. 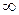 .
.
Список литературы
1. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1969. – 440с.;
2. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах – М.: Физматлит, 2001.
3. Виленкин Н.Я. и др. Задачник по курсу математического анализа, ч.1.– М.: Просвещение, 1971. – 343 с.;
4. Давыдов Н.А. и др. Сборник задач по математическому анализу.–М.: Просвещение, 1973. – 256 с.;
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.; Высшая школа, 2000, ч. I, II.
6. Ильин В.А., Позняк Э.Г. Линейная алгебра – М.: Наука, 1999.
7. Казаров С.А. Математический анализ. Ч.1. Введение в анализ. – Астрахань: Изд-во АГПИ, 1985. – 45 с.;
8. Кремер Н.Ш. Высшая математика для экономистов.– М.: ЮНИТИ, 1997. – 479 с.;
9. Кремер Н.Ш., Тришин И.М., Путко Б.А. и др. Практикум по высшей математике для экономистов. М.: ЮНИТИ, 2005. – 479 с.;
10. Лысенко Ф.Ф., Калабухова С.Ю. Математика. Подготовка к ЕГЭ-2013. –Ростов-на-Дону, Легион, 2013. – 410 с.
11. Кудрявцев Л.Д. Краткий курс математического анализа: В 2-х т.: Т.1. Дифференциальное и интегральное исчисления функции одной переменной. Ряды.–Висагинас: «Alfa», 1998.–400с.;
12. Письменный Д.Т. Конспект лекций по высшей математике. – М.; Рольф, 2002, ч. I, II.
13. Проскуряков И.В. Сборник задач по линейной алгебре – М.: Наука, 1984.
14. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре – М.: Наука, 1968.
15. Шипачев В.С. Высшая математика. – М.; Высшая школа, 1998.
 2015-04-01
2015-04-01 858
858







