Несобственные интегралы являются обобщением понятия определённого интеграла на случаи: 1) когда область интегрирования является не отрезок 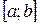 , а полупрямые
, а полупрямые 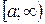 ,
, 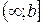 или вся прямая
или вся прямая 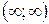 ; 2) когда функция имеет точки разрыва 2-го рода, в окрестностях которых функция неограниченна.
; 2) когда функция имеет точки разрыва 2-го рода, в окрестностях которых функция неограниченна.
Если функция 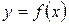 непрерывна на полупрямой
непрерывна на полупрямой 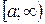 , то
, то 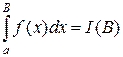 – некоторая непрерывная функция от
– некоторая непрерывная функция от 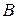 . Тогда предел
. Тогда предел 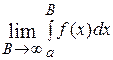 называется несобственным интегралом с бесконечным верхним пределом функции
называется несобственным интегралом с бесконечным верхним пределом функции 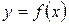 на
на 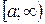 и обозначается
и обозначается 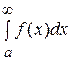 .
.
Таким образом 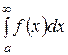 =
= 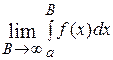 .
.
Если предел существует и конечен, то интеграл сходящийся, если не существует или бесконечен, то расходящийся. Аналогично определяется несобственный интеграл с бесконечным нижним пределом и несобственный интеграл с обоими бесконечными пределами:
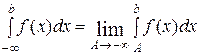 ,
, 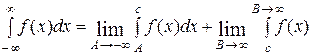 ,
,
где 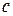 – произвольная фиксированная точка. При этом говорят, что интеграл сходится, если сходится каждый из двух несобственных интегралов в правой части этого равенства, и расходится, если хотя бы один из них расходится.
– произвольная фиксированная точка. При этом говорят, что интеграл сходится, если сходится каждый из двух несобственных интегралов в правой части этого равенства, и расходится, если хотя бы один из них расходится.
Если сходится интеграл 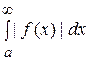 , то интеграл
, то интеграл 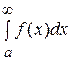 – абсолютно сходящийся.
– абсолютно сходящийся.
Для установления сходимости интеграла можно использовать следующие признаки сравнения.
Теорема. Пусть всюду на полупрямой 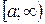 справедливо неравенство
справедливо неравенство 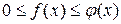 . Тогда: 1) если интеграл
. Тогда: 1) если интеграл 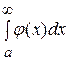 – сходится, то сходится и интеграл
– сходится, то сходится и интеграл 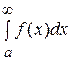 , причем
, причем 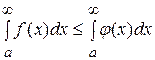 ; 2) если интеграл
; 2) если интеграл 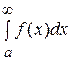 расходится, то будет расходиться и интеграл
расходится, то будет расходиться и интеграл 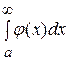 .
.
Пусть функция 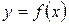 непрерывна во всех точках
непрерывна во всех точках 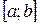 за исключением точки
за исключением точки 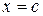
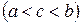 , где она терпит бесконечный разрыв. Тогда по определению
, где она терпит бесконечный разрыв. Тогда по определению
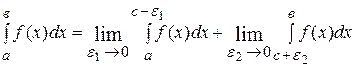 , где
, где 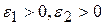 .
.
Интеграл называется несобственным интегралом от разрывной функции. Если оба предела, стоящие в правой части, существуют и конечны, то интеграл сходящийся, если хотя бы один из них не существует или бесконечен, то расходящийся. В случае, когда 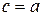 или
или 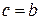 , в правой части равенства будет только один предел.
, в правой части равенства будет только один предел.
Теорема. Пусть всюду на отрезке 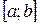 функции
функции 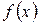 ,
, 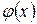 терпят бесконечный разрыв в точке
терпят бесконечный разрыв в точке 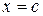 и всюду, кроме
и всюду, кроме 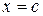 , выполняется неравенство
, выполняется неравенство 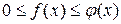 . Тогда: 1) если интеграл
. Тогда: 1) если интеграл 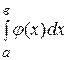 – сходится, то сходится и интеграл
– сходится, то сходится и интеграл 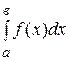 ; 2) если интеграл
; 2) если интеграл 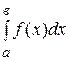 расходится, то будет расходиться и интеграл
расходится, то будет расходиться и интеграл 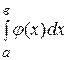 .
.
 2015-04-01
2015-04-01 943
943







