Пример 1. 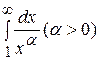 . Установить при каких значениях
. Установить при каких значениях 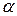 этот интеграл сходится, а при каких расходится.
этот интеграл сходится, а при каких расходится.
Решение. Пусть 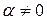 . Тогда
. Тогда 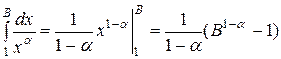 .
.
Итак, 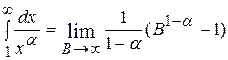 . Следовательно, если
. Следовательно, если 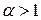 , то
, то 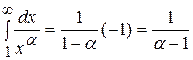 (т.к.
(т.к. 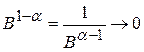 при
при 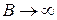 ), т.е. интеграл сходится; если
), т.е. интеграл сходится; если 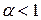 , то
, то 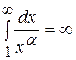 (т.к.
(т.к. 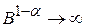 при
при 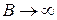 ), т.е. интеграл расходится.
), т.е. интеграл расходится.
При 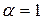
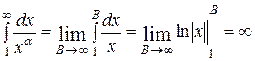 , т.е. интеграл расходится.
, т.е. интеграл расходится.
Пример 2. Доказать, что 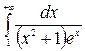 сходится.
сходится.
Решение. Известно, что при 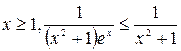 . Тогда
. Тогда 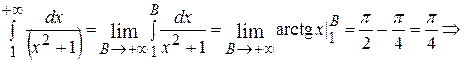
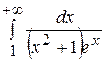 – сходится.
– сходится.
Пример 3. Исследовать на сходимость интеграл 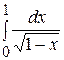 .
.
Решение. Подынтегральная функция терпит бесконечный разрыв при 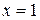 , следовательно, по определению:
, следовательно, по определению:
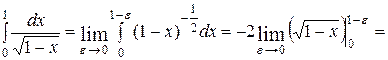
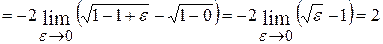 . Интеграл сходится.
. Интеграл сходится.
Пример 4. Найти условия сходимости и расходимости несобственных интегралов 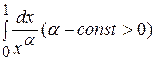 .
.
Решение. Подынтегральная функция терпит бесконечный разрыв при 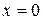 .
.
Пусть 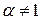 .
.
Тогда 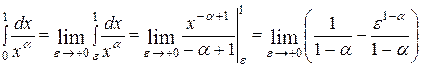 и если
и если 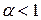 , то
, то 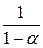 ;если
;если 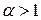 , то
, то 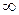 .
.
Пусть 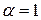 . Тогда
. Тогда
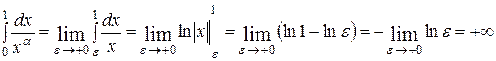 .
.
Итак, данный интеграл сходится при 
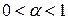 и расходится при
и расходится при 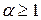 .
.
 2015-04-01
2015-04-01 2930
2930
