На корпусе судна при криволинейном движении

Теоретические методы исследования гидродинамических сил вязкостной природы, действующих на корпус судна, при криволинейном движении с углом дрейфа не позволяет достаточно точно определить величину гидродинамических сил. Поэтому задача определения гидродинамических сил на корпусе судна решается в основном на основе экспериментальных исследований на моделях судов.

Существует достаточно большое число методик определения гидродинамических сил на корпусе судна /4, 5/, /11/, /2, 8/. Эти методики различаются по форме представления гидродинамических характеристик корпуса, по типам судов, по величине кривизны траектории и по величине угла дрейфа.

Для случаев движения судна по траектории умеренной кривизны с малыми углами дрейфа применяется следующая форма определения гидродинамических сил:

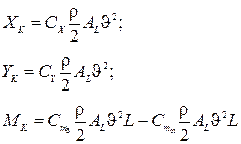(2.18)

где 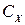, , 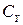, 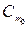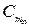- безразмерные коэффициенты гидродинамических сил, зависящие от 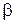, 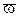и характеристик судна; 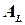- площадь диаметрального батокса, равная 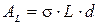; 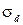- коэффициент полноты площади диаметрального батокса.

В соответствии с законами гидромеханики коэффициенты 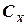, , 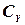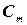для данного корпуса зависят от угла дрейфа, относительной угловой скорости вращения и критериев гидродинамического подобия. Экспериментально установлено, что число Фруда оказывает заметное влияние только при 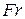> 0,25. Число Рейнольдса оказывает влияние на эти коэффициенты только при малых значениях: 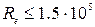. Поэтому для натурного судна заведомо применимо явление автомодельности. В практических расчетах управляемости крупных водоизмещающих судов используется допущение о стационарности потока воды, обтекающего корпус. В соответствии с этим допущением пренебрегают влиянием числа Струхаля.

Отмеченные обстоятельства позволяют для крупных водоизмещающих судов определять коэффициенты гидродинамических сил только от угла дрейфа, играющего роль угла атаки, и относительной угловой скорости вращения корпуса. Это в значительной степени облегчает как теоретические, так и экспериментальные способы определения этих коэффициентов.

Гидродинамические силы и момент, действующие на корпус судна при прямолинейном движении с углом дрейфа, называют позиционными. Коэффициенты позиционных сил и момента зависят только от угла дрейфа: ; ; .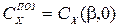

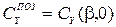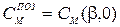Гидродинамические силы и момент, действующие на корпус при криволинейном движении, называют вращательными. Коэффициенты вращательных сил зависят от относительной угловой скорости вращения и от угла дрейфа: ; ; .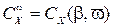

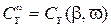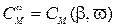Полные значения коэффициентов гидродинамических сил на корпусе равны сумме позиционных и вращательных коэффициентов.

Такое разделение коэффициентов на позиционные и вращательные составляющие обусловлено теоретическими и экспериментальными возможностями их определения. Так, в опытовом бассейне и в аэродинамической трубе возможно определение только позиционных составляющих сил. Вращательные же составляющие определяются на специальных созданных для этих целей экспериментальных установках в ротативных бассейнах, где модели судна создается движение по круговой траектории.

Разложим зависимост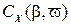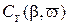и , и 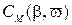в степенной ряд Маклорена с удержанием в разложении членов до 3-го порядка малости / 2 /:

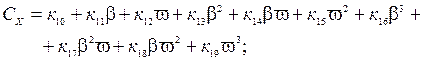
(2.19)

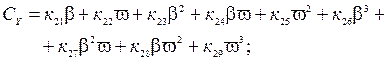
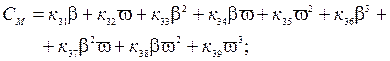
Коэффициенты 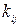в разложениях (2.19) называются гидродинамическими коэффициентами корпуса. Их значения подлежат определению. Применяют как теоретические методы, так и экспериментальные. Возможен прямой эксперимент с моделью данного корпуса. Также возможно использование данных систематизированных испытаний моделей судов разных типов в форме эмпирических зависимостей или диаграмм.

В имеющихся источниках приведены инженерные методики определения гидродинамических коэффициентов корпуса, различающиеся по типам судов и по авторским признакам. Выражения (2.19) являются общими и все частные методики со своими оригинальными обозначениями укладываются в эту схему. Область применения выражений (2.19) охватывает малые углы дрейфа и умеренные значения относительной угловой скорости вращения:

│b│ ≤ 0,5; │ 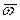│ ≤1,0. (2.20)

Характерный вид зависимостей 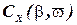, 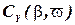показан на рис.2.4. Для этих коэффициентов характерно слабое влияние на них относительной угловой скорости .

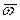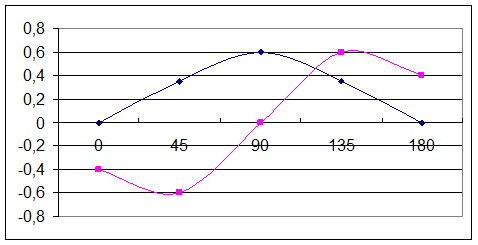
Рис. 2.4. Зависимост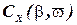и и .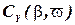

Характерный вид зависимостей 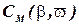показан на рис. 2.5.

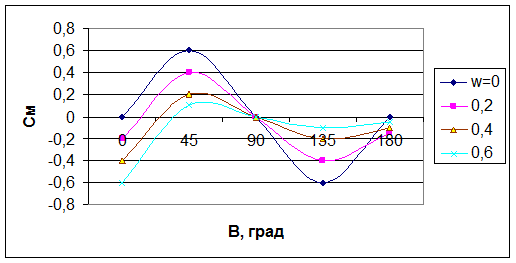
Рис. 2.5. Зависимости .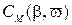

Р.Я. Першиц /4, 5, 9/ рекомендует принимать для морских транспортных судов при , ,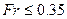

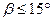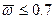
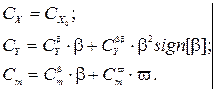(2.21)

Коэффициенты 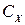, , 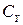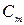отнесены здесь к условной площади диаметрального батокса 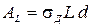, где 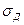- приведенный коэффициент полноты / /, определяемый по формуле:

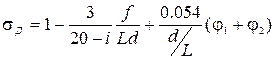. (2.22)

Коэффициенты аппроксимации (2.21) по рекомендации / 2 / можно определить по формулам:

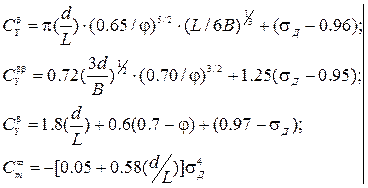(2.23)

Г.В. Соболев / 11, 2 / для морских транспортных судов при b < 15⁰, 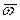< 0,8 предложил для коэффициентов 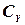, 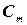следующие зависимости:

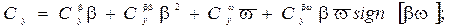
(2.24)

,

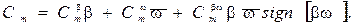в которых обозначено:

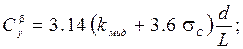
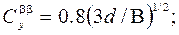
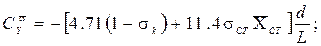(2.25)

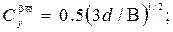
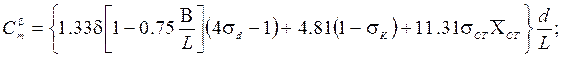
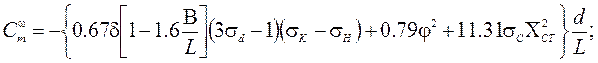
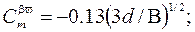
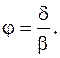
В зависимостях (2.25) обозначено:

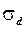- коэффициент полноты диаметрального батокса;

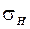- коэффициент полноты носовой части диаметрального батокса;

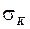- коэффициент полноты кормовой части диаметрального батокса;

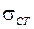- относительная площадь дейдвуда или стабилизатора, равная

;

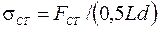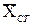- относительное отстояние ЦТ площади дейдвуда или стабилизатора от мидель-шпангоута;

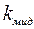- коэффициент, определяемый в зависимости от коэффициента полноты площади мидель-шпангоута 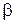и отношения 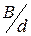по графику / 11 /.

Коэффициенты 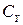, 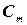отнесены к площади погруженной части диаметрального батокса .

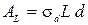При применении данной методики следует использовать форму уравнений движения корпуса (2.3).

В.Н. Коган и А.Д. Гофман / 6, 14 / для судов внутреннего плавания рекомендуют зависимость:

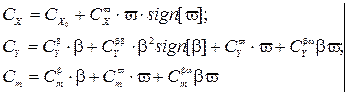(2.26)

Коэффициенты 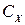, , 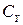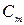отнесены к условной площади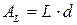

Коэффициенты аппроксимации определяются по формулам:

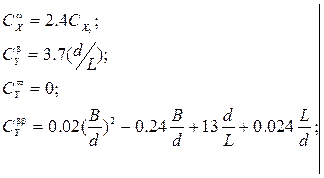(2.27)

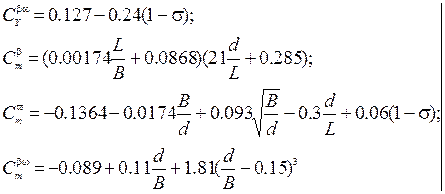(2.27)

В формах (2.27) предполагается коэффициент 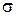определять по формуле

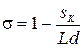(2.28)

в которой 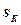- площадь кормового подзора.

Зависимости (2.26) справедливы при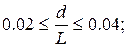

.

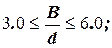
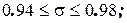
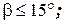
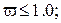
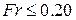В условиях мелководья гидродинамические силы на корпусе существенно зависят от относительной осадки (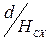). Влияние мелководья по данным В.И. Когана / 14, 2 / можно охарактеризовать с помощью коэффициентов:

; ; ; ;

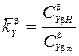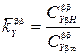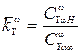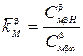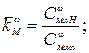
Для судов внутреннего и смешанного плавания:

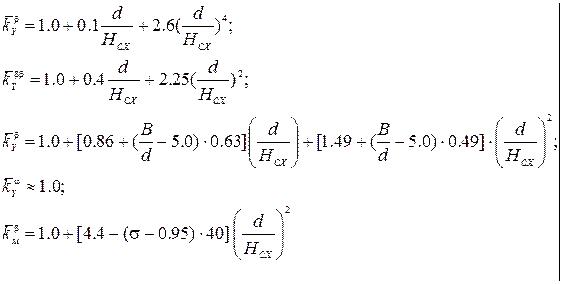(2.29)

Существуют и другие методики определения 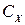, 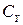и 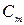/ 2 /, для случаев движения судна по криволинейной траектории с умеренными значениями 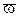и .

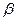Рассмотрим влияние течения на параметры движения судна. Течение характеризуется скоростью 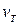и углом 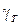в неподвижной системе координат. В общем случае 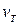и 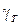являются переменными величинами, зависящими от координат x, h, а в некоторых случаях и по глубине водоема. В расчетной практике часто ограничиваются рассмотрением двух расчетных ситуаций, связанных с учетом течения: равномерное течение с 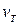=const и 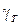=const; круговой канал с заданным радиусом судового хода 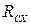при 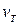=const.

Для судна, находящегося в однородном стационарном поле течения, в работе считается возможным рассматривать течение как некоторую переносную скорость в уравнениях движения корпуса. Возможен, однако, и гидродинамический подход к учету течения при определении гидродинамических сил и траектории движения.

Рассмотрим вначале случай, когда течение является однородным поступательным потоком. Пусть 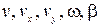- параметры движения корпуса, определяемые в связанной с корпусом системе координат; 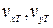- проекции скорости течения на оси связанной с корпусом системы координат. Тогда параметры движения корпуса судна относительно воды будут определяться следующей совокупностью формул:

;

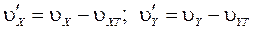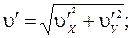(2.30)

; .

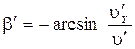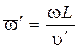Очевидно, что гидродинамические силы неинерционной природы следует определять в зависимости от параметров относительного движения корпуса: 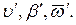Также, в зависимости от метода определения гидродинамических сил, следует ввести поправки и к инерционным гидродинамическим силам:

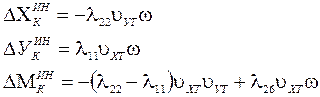(2.31)

Рассмотрим случай, характерный для течения воды в круговом канале. Движение судна можно рассматривать вдоль линии тока с радиусом 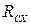. Проекции скорости течения на оси связанной системы координат будут равны:

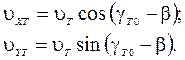(2.32)

В зависимостях (2.3) 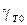- угол течения на входе в закругление, равный 0 при попутном течении и p при встречном течении.

На закруглении судового хода имеет место изменение угловой скорости вращения судна относительно воды, равное:

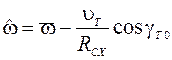(2.33)

В зависимости (2.33) радиус кривизны судового хода Rсх имеет знак (+) при правом повороте и знак (-) при левом повороте.

К гидродинамическим силам на корпусе дополнительно необходимо прибавить силу соскальзывания Кориолиса, равную

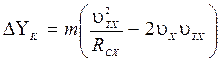(2.34)

Проведем анализ зависимостей (2.21 – 2.29) коэффициентов гидродинамических сил и момента на корпусе судна от параметров 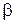и 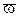при знакопеременных их значениях. Это необходимо для расчета зигзагообразных маневров.

Вначале рассмотрим функцию 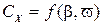. Эта функция обладает такими свойствами:

1. При движении прямым курсом ()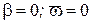

.

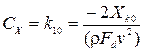2. При изменении знака угла дрейфа знак позиционного коэффициента 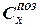не изменяется

.

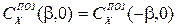3. Экспериментальные исследования гидродинамических характеристик корпуса судна показывают, что продольная сила 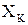мало зависит от угловой скорости вращения .

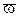Коэффициент поперечной силы 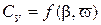обладает следующими свойствами:

1. При движении корпуса на прямом курсе (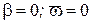) ввиду симметрии корпуса относительно ДП поперечная сила равна нулю

.

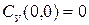2. Знак позиционного коэффициента 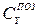изменяется при изменении знака угла дрейфа

.

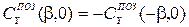3. Аналогично, при изменении только знака 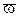, вращательный коэффициент 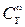изменяет свой знак:

.

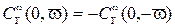4. При одновременном изменении знаков 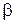и :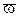

.

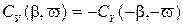Коэффициент момента 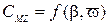обладает следующими свойствами:

1. При движении корпуса на прямом курсе (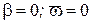) ввиду симметрии корпуса относительно ДП момент равен нулю

.

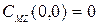2. Знак позиционного коэффициента 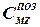изменяется при изменении знака угла дрейфа:

.

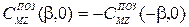3. Аналогично, при изменении только знака 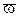, вращательный коэффициент 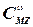изменяет свой знак:

.

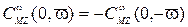4. При одновременном изменении знаков 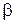и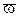

.

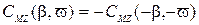Эти свойства коэффициентов гидродинамических сил на корпусе судна должны бы быть учтены при обработке экспериментальных данных ротативных и других испытаний моделей судов. Есть опасения на этот счет, поскольку испытания моделей часто проводятся только для положительных значени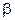й и 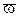, что вполне достаточно для расчета циркуляций одного знака и для удовлетворения основных критериев управляемости судна.

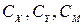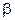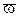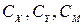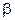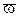С целью проверки отмеченных свойств коэффициентов , для различных судов, подпадающих под указанные методы определения, была разработана программа Rsil.exe и выполнен расчет этих коэффициентов при различных значениях и , в том числе и при отрицательных значениях. Кроме того, осуществлена проверка на монотонный характер изменения коэффициентов в зависимости от и . Рассмотрение результатов этих расчетов показал: данные методы определения коэффициентов гидродинамических сил на корпусе судна в основном (за исключением ситуаций разных знаков 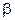и 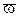) корректны относительно перечисленных свойств коэффициентов и могут быть применены для исследования знакопеременных маневров судов.