Оптимальное управление непрерывными динамическими системами

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика С.П.КОРОЛЕВА»

Ю. Заболотнов

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ НЕПРЕРЫВНЫМИ ДИНАМИЧЕСКИМИ СИСТЕМАМИ

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

САМАРА 2005

УДК 519.9+534.1

Рецензенты: С.А. Ишков, Л.В. Кудюров

Заболотнов Ю.

Оптимальное управление непрерывными динамическими системами: учеб. пособие / Ю. Заболотнов; Самар. гос. аэрокосм. ун-т. Самара, 2005. 149 с.: ил.

Пособие включает в себя описание методов оптимального управления динамическими системами. Особое внимание уделено оптимальному решению задачи стабилизации для линейных динамических систем. Наряду с изложением классических методов оптимального управления линейными системами, основанными главным образом на принципе динамического программирования Беллмана, рассматривается приближенно оптимальное управление колебательными динамическими системами с использованием метода усреднения.

Материал пособия входит в курс лекций «Теоретические основы автоматизированного управления», читаемых автором для студентов специальности 230102 – автоматизированные системы обработки информации и управления на кафедрах информационных систем и технологий, математики и механики СГАУ. Однако пособие может быть полезно для студентов других специальностей при изучении теории оптимального управления динамическими системами.

ОГЛАВЛЕНИЕ

ПРЕДИСЛОВИЕ ……………………………………………………. 5

1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ СИСТЕМАМИ ………………………….………………………….. 8

1.1. Постановка задачи оптимального управления динамическими системами …………………………….…...8

1.2. Программное оптимальное управление и задача

стабилизации ………………………………………………………. 11

1.3. Невозмущенное и возмущенное движения динамической системы …………………………………………….………….. 12

1.4. Постановка задачи оптимальной стабилизации движения для линейной динамической системы.……………………………..… 14

2. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ

ДИНАМИЧЕСКИХ СИСТЕМ ………………………………….….16

2.1. Подобные преобразования линейных динамических систем.16

2.2. Управляемость динамических систем.……………………….18

2.3. Наблюдаемость динамических систем ……………………….21

3. ПРИНЦИП ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ БЕЛЛМАНА И ТЕОРИЯ УСТОЙЧИВОСТИ ЛЯПУНОВА …….24

3.1. Принцип динамического программирования Беллмана …….24

3.2. Оптимальное управление линейными динамическими системами ………………………………………………..………… 29

3.3. Теория устойчивости Ляпунова ………………………………31

3.4. Связь метода динамического программирования с теорией устойчивости Ляпунова …………………………………………... 37

4. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДЛЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ …………………… 39

4.1. Решение уравнения Беллмана для линейных стационарных динамических систем..…………………………………………… 39

4.2. Решение уравнения Беллмана для линейных нестационарных динамических систем..…………………………………………… 41

4.3. О выборе критерия оптимальности при решении задачи стабилизации ……………………………………………………….43

4.4. Пример оптимального выбора коэффициентов регулятора

при управлении линейной системой второго порядка....……….. 47

5. ДИНАМИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ ………….56

5.1. Малые колебания динамических.истем…………………….…56

5.2. Управляемость и наблюдаемость линейных колебательных динамических систем ………………………………………………. 65

5.3. Метод малого параметра..…………………………………….. 68

5.4. Метод усреднения..………………………………………….… 72

5.5. Метод усреднения для системы с одной степенью свободы.. 76

5.6. Метод усреднения для систем с несколькими быстрыми

фазами ………………………………………………………………. 79

5.7. Метод усреднения для системы с двумя степенями

свободы ………………………………………………………..…… 86

6. ПРИБЛИЖЕННО ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ КОЛЕБАТЕЛЬНЫМИ СИСТЕМАМИ.... 93

6.1. Управление линейной колебательной системой с одной степенью свободы ……………………………………………….… 93

6.2. Управление линейной колебательной системой с двумя степенями свободы..………………………………………………. 106

6.3. Влияние нелинейных возмущений на решение задачи оптимального управления …………//…………………………… 115

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ …..…………127

ПРИЛОЖЕНИЕ 1. Подобные преобразования линейных динамических систем …………………………………………..…129

ПРИЛОЖЕНИЕ 2. Качественное исследование линейных динамических систем на фазовой плоскости …………………… 134

ПРИЛОЖЕНИЕ 3. Дифференцирование функций с векторным аргументом ………………………………………………………... 142

ПРИЛОЖЕНИЕ 4. Основные понятия теории асимптотических рядов ………………………………………………………………. 143

ПРИЛОЖЕНИЕ 5. Усреднение тригонометрических

функций ………………………………………..………………….. 148

ПРЕДИСЛОВИЕ

Традиционно в классической теории управления рассматриваются две основные задачи: задача определения программного движения динамической системы и задача о проектировании регуляторов, реализующих заданное программное движение объекта управления (задача стабилизации). Основное внимание в пособии уделяется решению задачи стабилизации, при решении которой обычно используются линейные динамические модели. По сравнению со статическими системами в динамических системах процесс развивается во времени и управление в общем случае тоже является функцией времени.

При решении задачи стабилизации могут быть использованы различные методы. Здесь, прежде всего, следует отметить классические методы теории автоматического управления, основанные на аппарате передаточных функций и частотных характеристик. Однако появление быстродействующих ЭВМ привело к развитию новых методов, составляющих основу современной теории управления. В современной теории управления поведение системы описывается в пространстве состояний и управление системой сводится к определению оптимальных в некотором смысле управляющих воздействий на систему в каждый момент времени. Причем математическими моделями непрерывных динамических систем обычно являются системы обыкновенных дифференциальных уравнений, независимой переменной в которых является время.

При решении задачи стабилизации оптимальность управления понимается в смысле минимума некоторого критерия оптимальности (функционала), который записывается в виде определенного интеграла. Критерий оптимальности может характеризовать различные аспекты качества управления: затраты на управление (энергии, топлива и др.), ошибки управления (по различным переменным состояния) и т.д. Для определения оптимального управления при решении задачи стабилизации используется классический принцип динамического программирования Беллмана.

Первый раздел пособия является вводным: в нем производится математическая постановка задач, решаемых при управлении непрерывными динамическими системами. Второй раздел посвящен вопросам, предваряющим построение оптимального управления для линейных систем: вопросам управляемости и наблюдаемости. В третьем разделе выводятся основные соотношения принципа динамического программирования Беллмана, из которых далее определяется оптимальное управление для линейной динамической системы при решении задачи стабилизации. В этом же разделе показывается, что принцип динамического программирования Беллмана для линейных систем органически связан со вторым методом Ляпунова, выполнение теорем которого обеспечивает решение задачи стабилизации. В четвертом разделе пособия излагаются алгоритмы определения оптимального управления при решении задачи стабилизации при заданном квадратичном критерии оптимальности (подынтегральная функция функционала является квадратичной формой от управления и переменных состояния системы). Приводится пример определения оптимального управления с заданным критерием оптимальности для конкретной линейной системы. В пятом разделе излагаются основы теории динамических колебательных систем. Выводятся основные соотношения принципа усреднения, позволяющего во многих случаях существенно упростить анализ и синтез колебательных систем. В шестом разделе рассматривается метод определения приближенно оптимального управления для задачи стабилизации колебательными системами. Приводятся примеры управления колебательными системами с одной и с двумя степенями свободы. Анализируются вопросы возможного влияния нелинейных возмущений на решение задач стабилизации колебательных систем.

Методы, изложенные в пособии, позволяют найти оптимальное управление для решения задач стабилизации динамических систем в виде аналитических функций, зависящих от переменных состояния системы. В этом случае говорят, что решается задача синтеза управления. Эти методы можно отнести к теории аналитического конструирования регуляторов, являющейся одной из важных направлений развития современной теории управления.

Материал пособия основывается на работах в области теории управления, которые с течением времени уже стали классическими. Здесь прежде всего необходимо отметить работы Понтрягина Л.С. [2], Летова А.М. [3], Демидовича Б.П. [4], Гропа Д. [6], Беллмана Р. [7], Моисеева Н.Н.[13], Боголюбова Н.Н., Митропольского Ю.А. [14] и др. известных отечественных и зарубежных ученых.

1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ СИСТЕМАМИ

1.1. Постановка задачи оптимального управления динамическими системами

Математические модели динамических систем могут быть построены в различных формах. Это могут быть системы обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, соответствующие дискретные модели и др. Отличительной особенностью математического описания любой динамической системы является то, что ее поведение развивается во времени и характеризуется 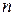функциями 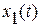,… , 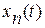которые называются переменными состояния (фазовыми координатами) системы. В дальнейшем будем рассматривать системы с непрерывным временем. Движение динамической системы может быть управляемым и неуправляемым. При реализации управляемого движения поведение динамической системы зависит также от 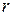управляющих функций 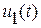,… 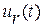. Предположим также, что поведение системы определяется однозначно, если задана вектор-функция управления 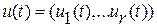и начальное фазовое состояни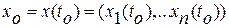е , где 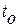- начальное время.

В качестве математической модели динамической системы будем рассматривать систему обыкновенных дифференциальных уравнений, записанную в нормальной форме Коши

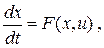(1.1)

где 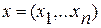, , 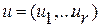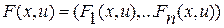- известная вектор-функция.

К системе (1.1) чаще всего приводятся разнообразные математические модели динамических систем с непрерывным временем. Так, например, если поведение динамической системы описывается системой дифференциальных уравнений в частных производных и происходит в пространстве и во времени (математические модели механики сплошной среды), то, производя дискретизацию по пространству (конечно элементный подход), приходим к системе обыкновенных дифференциальных уравнений подобной (1.1), решение которой ищутся как функции времени.

Введенное ранее предположение об однозначности процесса управления для системы (1.1) определяется выполнением условий теоремы о существовании и единственности решений систем обыкновенных дифференциальных уравнений в форме Коши [1].

Сформулируем задачу оптимального управления системой (1.1) [2]. В начальный момент 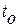система (1.1) находится в состоянии 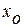, необходимо определить такое управление 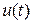, которое переведет систему в заданное конечное состояние 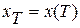(отличное от начального), где 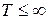- конечное время. Обычно требуется, чтобы переход из точки 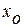в точку 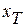(переходный процесс) был в определенном смысле наилучшим из всех возможных переходов. Например, если рассматривается некоторая техническая система, то переходный процесс должен удовлетворять условию минимума затраченной энергии или условию минимума времени перехода. Такой наилучший переходный процесс принято называть оптимальным процессом.

Функция управления 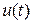обычно принадлежит некоторой области управления 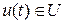, которое является множеством 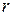-мерного евклидова пространства. В технических приложениях предполагают, что область 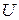есть замкнутая область, то есть область, включающая свои границы. Допустимым управлением будем называть любое управление 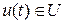, переводящее систему из точки 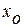в точку 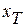. Для количественного сравнения различных допустимых управлений вводят критерий оптимальности, который, как правило, представляют в виде некоторого функционала

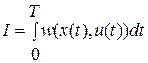. (1.2)

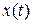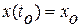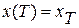Функционал вычисляется на решениях системы (1.1) , удовлетворяющих условиям и , при заданном допустимом управлении .

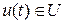Окончательно, задача оптимального управления формулируется следующим образом: в фазовом пространстве даны две точк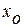и и 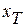; среди всех допустимых управлений 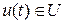, переводящих фазовую точку из положения 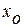в положение 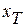, найти такое, для которого функционал (1.2) принимает наименьшее значение.

Управление 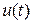, дающее решение поставленной выше задачи, называется оптимальным управлением и обозначается 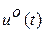, а соответствующая траектория 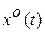- оптимальной траекторией.

Замечание. Если необходимо обеспечить максимум некоторого критерия, то можно свести данную задачу к задаче поиска минимума формально изменив знак перед функционалом (1.2).

Частным случаем поставленной задачи оптимального управления является случай, когда 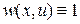. Тогда функционал (1.2) принимает вид 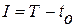и оптимальность заключается в реализации минимального времени перехода из точки 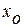в точку 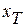. Такую задачу оптимального управления называют задачей быстродействия.

1.2. Программное оптимальное управление и задача стабилизации

Рассмотрим движение динамической системы (1.1). Пусть для этой системы найдено оптимальное управление 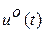и получена соответствующая оптимальная траектория 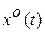. При реализации оптимальной траектории в технических задачах неизбежно наталкиваются на существенные трудности, заключающиеся в невозможности, во-первых, точно установить реальную систему (или объект управления) в начальное состояние 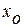, во-вторых, точно реализовать само оптимальное управление 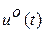, в третьих, точно предсказать заранее внешние условия функционирования системы (приближенность исходной математической модели). Все это приводит к необходимости решать задачу о коррекции закона оптимального управления в процессе функционирования любой технической системы (или объекта). Таким образом, задачу оптимального управления в реальных условиях можно разделить на две части: 1) построение номинального оптимального управления 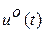исходной динамической системой в идеальных условиях в рамках математической модели (1.1); 2) построение корректирующих управляющих воздействий 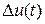с целью реализации заданного номинального оптимального управления 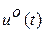и оптимальной траектории 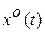в процессе функционирования системы. Первую часть задачи оптимального управления принято называть задачей построения оптимального программного управления [3], причем она решается в рамках априорной информации, известной заранее о рассматриваемой системе. Вторую часть задачи называют задачей стабилизации заданной номинальной программы управления [3] и решаться она должна в процессе функционирования системы по информации, поступающей от измерительных устройств системы управления. Задача стабилизации номинальной программы управления тоже может быть поставлена как задача поиска оптимального управления 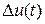по соответствующему критерию, что будет сделано ниже (см. раздел 1.4).

Замечание. Очевидно, что в качестве номинальной программы управления может быть использована не только оптимальное управление 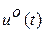, но и любое другое допустимое управление (если задача оптимизации программного управления не решается). В частном самом простом случае может быть, например, поставлена задача о стабилизации некоторого постоянного положения системы .

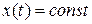1.3. Невозмущенное и возмущенное движения динамической системы

Так как реальное движение системы неизбежно отличается от номинального программного, то этот факт привел к концепции невозмущенного и возмущенного движений Ляпунова А.А. [4]. Так, любое программное движение системы (1.1), независимо от того является ли оно оптимальным или допустимым называется невозмущенным движением. Причем этому движению соответствует некоторое частное решение системы (1.1). Возмущенное движение оценивается при этом некоторыми отклонениями от невозмущенного движения. Следовательно, возмущенное движение будет описываться следующими переменными

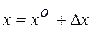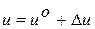, , (1.3)

где переменные 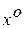и 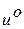характеризуют номинальную программу управления, а переменные 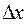и 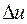- отклонения от номинальной программы.

Подставляя соотношения (1.3) в систему (1.1), получим

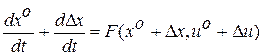. (1.4)

Прибавляя и отнимая в правой части системы (1.4) одинаковое слагаемое 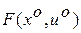и учитывая, что

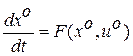, (1.5)

получим систему в отклонениях от номинального движения

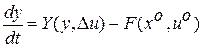, (1.6)

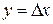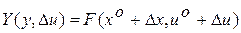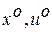где , , а определяются в результате решения системы (1.5).

Обычно считают, что отклонения 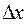и 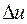от номинального движения являются малыми величинами. Поэтому, если разложить функцию 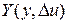в ряд Тейлора и ввести обозначения 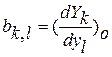, , 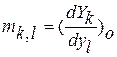где индекс (o) означает, что частные производные определяются для заданной номинальной программы, то получим

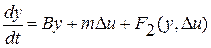. (1.7)

Здесь функция 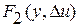определяет слагаемые второго порядка и выше по отклонениям 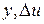; матрицы 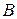и 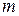выделяют линейную часть ряда и имеют компоненты 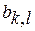и ; .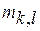

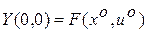Уравнения, записанные в отклонениях (1.7), имеют большое значение в теории управления. На основании этих уравнений производится постановка большого количества задач оптимизации, имеющих практический интерес. Одна из этих задач – задача стабилизации, сформулированная выше. При решении этой задачи требуется определить, как следует выбрать корректирующие управляющие воздействия 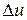, чтобы уменьшить отклонения 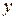в некотором смысле наилучшем образом.

1.4. Постановка задачи оптимальной стабилизации движения для линейной динамической системы

Чаще всего при решении задачи стабилизации движения системы или объекта управления используется линейная динамическая система в отклонениях, получающаяся из системы (1.7) отбрасыванием нелинейных слагаемых 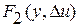. Тогда

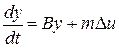, (1.8)

где матрицы 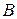и 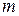в общем случае являются функциями времени, так как зависят от номинальной программы управления .

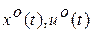Рассмотрим для простоты случай, когда управление 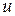является скалярной величиной. При рассмотрении задачи управления линейной динамической системой обычно в качестве критерия оптимальности применяется функционал с квадратичной подинтегральной функцией [3]

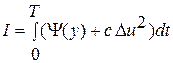. (1.9)

Здесь 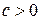, 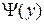- симметричная квадратичная форма вектора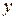

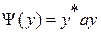, (1.10)

где 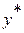- транспонированный вектор 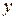(вектор-строка), 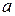- квадратная симметричная матрица.

Предполагается, что функция 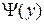есть положительно определенная квадратичная форма 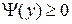, причем 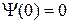только при 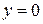. Проводя перемножения в соотношении (1.10) в скалярном виде можно записать

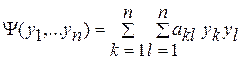, (1.11)

где 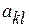- компоненты матрицы .

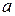Для того, чтобы квадратичная форма (1.11) была положительно определена необходимо и достаточно, чтобы все главные миноры вещественной симметричной матрицы 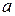были положительны (условие Сильвестра) [5]:

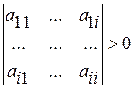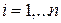, (1.12)

В качестве допустимых функций управления обычно принимаются кусочно-непрерывные функции 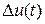, принадлежащие некоторой области 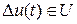. Если управление определяется как функция вектора фазовых переменных 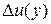, то говорят, что решается задача синтеза управления. После подстановки закона 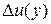в систему (1.8) получается автономная линейная система (правые части дифференциальных уравнений зависят только от вектора фазовых переменных 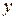), которая в теории управления называется замкнутой системой.

Таким образом, задача оптимальной стабилизации движения линейной динамической системой формулируется так: среди допустимых управлений 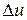системой (1.8) найти такое управление, которая доставляет минимум функционалу (1.9) и переводит систему из начального положения 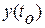в начало координат 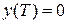, где 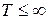- время перехода.

Если рассматривается частный случай, когда 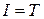, то задача называется задачей быстродействия.

2. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ДИНАМИЧЕСКИХ СИСТЕМ

2.1. Подобные преобразования линейных динамических систем

При исследовании движения линейных динамических систем вида (1.8) часто используются так называемые подобные преобразования. Пусть 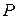- невырожденная квадратная матрица (см. Приложение 1). Введем линейную замену переменных

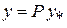. (2.1)

Рассмотрим преобразование системы (1.8), где матрицы 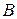и 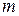для простоты будем считать постоянными, подставив замену (2.1) в соотношение (1.8). Тогда

,

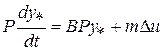или, умножая слева на обратную матрицу 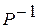, получим линейную систему относительно новых переменных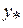

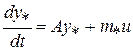, (2.2)

где 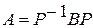, , 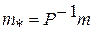и для сокращения обозначений полагается .

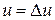Определение. Преобразование матрицы 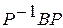, где квадратная матрица 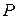не вырожденна, называется подобным преобразованием.

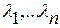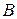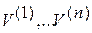Подобные преобразования матриц и, следовательно, линейных динамических систем обладают рядом важных свойств (см. Приложение 1). В частности, при подобных преобразованиях собственные значения матриц не изменяются. Пусть - собственные значения матрицы , а - соответствующие им собственные вектора (см. Приложение 1). Введем матрицу 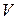, столбцами которой являются собственные вектора 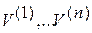. Рассмотрим случай, когда матрица 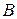не имеет кратных (одинаковых) собственных значений. В этом случае подобное преобразование 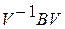приводит матрицу 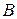к диагональному виду 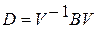, где 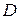- диагональная матрица, на главной диагонали которой стоят собственные значения 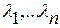матрицы 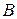(доказательство приводится в Приложении 1).