Приоритетной при заполнении таблицы является не северо-западная клетка, а клетка с наименьшей стоимостью перевозки. Этот метод обычно дает начальный план, более близкий к оптимальному.
Методом северо - западного угла исходную матрицу перевозок начинают заполнять с левого верхнего угла. В магазин В1 отправляем с первой базы груз в количестве 20 т, так как потребность этого магазина составляет 20 т, а запас товара на базе 50 т. Потребность магазина В1 в этом случае удовлетворена полностью, а на первой базе осталось груза 30 т. Поэтому оставшийся товар на первой базе (30 т) отправляют во второй магазин В2, имеющий потребность в 60 т груза. Оставшуюся потребность магазина В2 (30 т) удовлетворяют, перевозя груз со второй базы А2. На базе А2 остался груз 60 т - его отправляют в магазин В3 (30 т) и в В4 (30 т). Потребность магазина В4 и В5 удовлетворится с базы А3.
Матрица перевозок примет вид табл. 2.7.
Подсчитаем число заполненных клеток 7. Их число равно m+n- 1=3+5–1=7. Таким образом, имеем невырожденный опорный план.
Таблица 2.7
| B1 | B2 | B3 | B4 | B5 | Запасы | |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Стоимость перевозок в полученном плане:
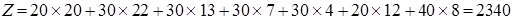 руб.
руб.
Методом наименьшей стоимости заполнение матрицы перевозок начинается с клетки, имеющей наименьший тариф (с клетки А2В4). В этом случае потребность магазина В4 составляет 50 т, а запас на базе А2 90 т. Поэтому в эту клетку следует отправить 50 т. Затем заполняем клетку А2В1, имеющей тариф 5, - 20 т. Следующая клетка с наименьшим тарифом А3В5 . Туда отправляем 40 т. и т.д. Получим таблицу 2.8.
Таблица 2.8
| B1 | B2 | B3 | B4 | B5 | Запасы | |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Стоимость перевозок в полученном плане:
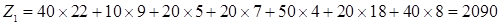 руб.
руб.
При применении метода наименьшей стоимости стоимость перевозки получается меньше по сравнению с методом северо- западного угла.
 2015-04-01
2015-04-01 817
817








