Требуется максимизировать функцию доходов:
Z = 4 x1 + 6 x2 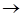 max
max
При наличии системы ограничений:
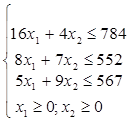
Сведем задачу на минимум к задаче на максимум. Для этого умножим функцию цели на (-1).
-Z =-4 x1 - 6 x2 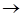 min
min
Для приведения задачи к каноническому виду (с ограничениями - равенствами), пригодному к решению симплекс - методом, вводим дополнительные переменные x3, x4, x5 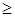 0.
0.
Имеем:
-Z = -4 x1 -6 x2 + 0 ×х3+ 0 ×х4+ 0 ×х5  min.
min.
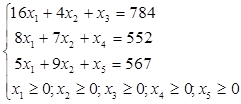
Дополнительные переменные x3, x4, x5 означают количество неиспользованного сырья (остаток) соответственно первого, второго и третьего вида.
Запишем задачу в векторной форме:
-Z = -4x1-6x2 +0×х3+0×х4+0×х5  min.
min.
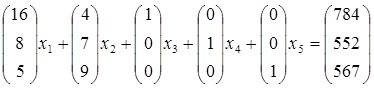 .
.
Коэффициенты при x3, x4, x5 образуют единичную матрицу. Принимаем вектора коэффициентов при x3, x4, x5 за базис.
Составим первую симплекс-таблицу (табл.2.2).
В столбец С запишем коэффициенты, стоявшие в целевой функции при соответствующих переменных (в нашем случае они равны нулю).
В столбец b поставим ограничения по ресурсам. Коэффициенты в столбцах а1, а2,…а5 – это коэффициенты, соответствующие переменным х1, х2,…х5 в системе ограничений, записанной в векторной форме.
Последняя строка называется индексной. Ее заполняют следующим образом. Находят сумму попарных произведений столбца b на С, затем вычитают соответствующий коэффициент при целевой функции.
Строка Zj-Cj: 0´784 + 0´552 + 0´567 = 0.
Столбец а1: 0´16 + 0´8 + 0´5 – (-4) = 4.
Столбец а2: 0´4 +0´7 + 0´6 – (-6) = 6.
Столбец а3: 0´1 +0´0 + 0´0 – 0 = 0 и т.д.
Таблица 2.2
| Базис | C | b | с1=-4 | с2=-6 | с3=0 | с4=0 | с5=0 |
| `a1 | `a2 | `a3 | `a4 | `a5 | |||
| `a3 | с3=0 | ||||||
| `a4 | с4=0 | ||||||
| `a5 | с5=0 | ||||||
| Zj-Cj |
Первое базисное решение находится в столбце b: x1 = 0; x2 = 0; x3 = 784; x4 = 552; x5 = 567. При этом Z = 0. В индексной строке имеются положительные числа 4, 6. Следовательно, план не оптимален.
Применяем алгоритм симплексного метода.
1. Выбираем максимальный по абсолютной величине элемент, стоящий в индексной строке. Этот элемент равен 6. Ему соответствует столбец а2. Этот столбец будем называть направляющим. Выделим его в симплексной таблице.
2. Выбираем направляющую строку. Для этого делим элементы столбца b на соответствующие числа направляющего столбца и находим минимальное частное. Т.е.
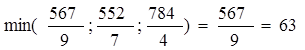 .
.
Минимальное частное соответствует третьей строке. Таким образом, направляющей строкой будет строка а5. Выделим ее.
Если в направляющем столбце стоят нули и отрицательные числа, то соответствующие строки не рассматриваются. Если все элементы столбца меньше или равны нулю, то нельзя выбрать направляющую строку и найти оптимальное решение.
3. Элемент, стоящий на пересечении направляющей строки и направляющего столбца называется разрешающим. В данном случае он равен 9.
4. Строим вторую симплексную таблицу. Для этого переменную, соответствующую разрешающему столбцу а2 введем в базис на место переменной а5.
5. Элементы направляющей строки делим на разрешающий и результаты вносим в соответствующую строку второй симплекс-таблицы. То есть в третьей строке второй симплексной таблицы (табл.2.3) получим:
(63; 5/9; 1; 0; 0; 1/9).
6. Элементы направляющего столбца, кроме разрешающего, равного теперь единице, заменяем нулями. Результат вносим в соответствующий столбец новой таблицы.
7. Все остальные элементы преобразуем по правилу прямоугольника. Для этого для каждого элемента исходной таблицы составим прямоугольник так, чтобы преобразуемый элемент и разрешающий располагались на одной из диагоналей прямоугольника. Преобразованное значение вычисляют по формуле (2.8).
То есть:
строка а3:
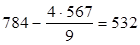 ;
; 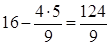 ;
; 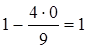 ;
; 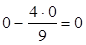 ;
; 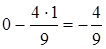 .
.
строка а4:
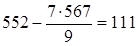 ;
; 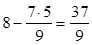 ;
; 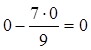 ;
; 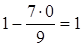 ;
; 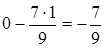 .
.
индексная строка:
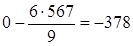 ;
; 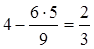 ;
; 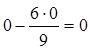 ;
; 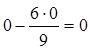 ;
; 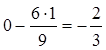 .
.
Таблица 2.3
| Базис | C | b | с1 =-4 | с2 =-6 | с3 =0 | с4 =0 | с5 =0 |
| a1 | a2 | a3 | a4 | a5 | |||
| a3 | 124/9 | -4/9 | |||||
| a4 | 37/9 | -7/9 | |||||
| a2 | -6 | 5/9 | 1/9 | ||||
| Zj-Cj | -378 | 2/3 | -2/3 |
Получили второе базисное решение: x1= 0; x2= 63; x3= 532; x4 =111; x5 =0 и -Z2 =-378(значение -378 находится на пересечении индексной строки и столбца из свободных членов). Это решение не оптимально, т.к. в индексной строке имеется положительный коэффициент 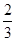 .
.
Повторяем процедуру симплексного метода.
Выбираем направляющий столбец (положительное число в индексной строке соответствует а1). Вводим в базис а1 в новой симплекс - таблице.
Выбираем направляющую строку, то есть находим:
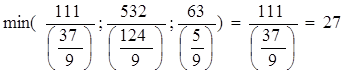 .
.
Направляющей строкой будет строка а4. Разрешающий элемент 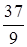 .
.
Составим третью симплекс-таблицу (табл.2.4).
Таблица 2.4
| Базис | C | b | с1 =-4 | с2 =-6 | с3= 0 | с4= 0 | с5= 0 |
| a1 | a2 | a3 | a4 | a5 | |||
| a3 | 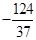 | 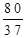 | |||||
| a1 | -4 | 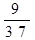 | 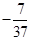 | ||||
| a2 | -6 | 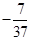 | 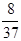 | ||||
| Zj-Cj | -396 | - 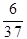 | - 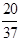 |
Получили третье базисное решение: x1= 27; x2= 48; x3= 16; x4= 0; x5= 0; -Z=- 396.
В индексной строке нет положительных коэффициентов. Решение оптимально.
Вывод. Максимальный суммарный доход равен Zmax =396 руб. Следует произвести 27 единиц продукции A и 48 единиц продукции вида В. При этом сырье первого вида останется неизрасходованным в количестве x3= 16 кг, а сырье второго и третьего вида будет израсходовано полностью x4= 0; x5= 0.
Заметим, что ранее тот же результат был получен геометрическим методом решения.
2.4 Транспортная задача
Транспортная задача является специальной задачей линейного программирования.
Имеется m баз (пунктов отправления) A1, A2,...,Am, в которых сосредоточены запасы однородного груза в количествах 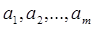 соответственно. Груз необходимо перевезти n потребителям (магазинов) B1, B2,..., Bn в количествах
соответственно. Груз необходимо перевезти n потребителям (магазинов) B1, B2,..., Bn в количествах 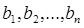 соответственно. Известна стоимость
соответственно. Известна стоимость 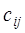 перевозки единицы груза с базы Ai
перевозки единицы груза с базы Ai 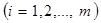 потребителю Bj
потребителю Bj 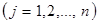 . Требуется спланировать перевозки грузов так, чтобы их общая стоимость была минимальная.
. Требуется спланировать перевозки грузов так, чтобы их общая стоимость была минимальная.
Определение. Транспортная задача называется задачей с выполненным балансом или транспортной задачей закрытого вида, если запасы груза на базах совпадают с потребностями потребителей, т.е.
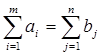 . (2.9)
. (2.9)
Рассмотрим закрытую модель транспортной задачи с матрицей перевозок, заданной в таблице 2.5.
Таблица 2.5
| Базы | Потребители | Запасы | |||
| B1 | B2 | ................. | Bn | ||
| A1 | c11 | c12 | . ................. | c1 n | a1 |
| A2 | c21 | c22 | . ................. | c2 n | a2 |
| ................ | . ............. | . ................ | . ................. | . ........ | . .................. |
| Am | cm1 | cm2 | . .................. | cm n | am |
| Потребности | b1 | b2 | . ................ | bm | 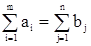 |
 2015-04-01
2015-04-01 886
886








