Пусть функция  определена на промежутке
определена на промежутке 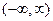 , кусочно непрерывна вместе со своей производной в любом конечном промежутке и абсолютно интегрируема.
, кусочно непрерывна вместе со своей производной в любом конечном промежутке и абсолютно интегрируема.
Определение. Формула 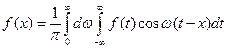 ,
,
называется формулой Фурье, а интеграл в правой части формулы – интегралом Фурье для функции  .
.
Равенство имеет место в точках непрерывности функции  ; в точках разрыва данной функции интеграл Фурье равен среднему арифметическому ее односторонних пределов:
; в точках разрыва данной функции интеграл Фурье равен среднему арифметическому ее односторонних пределов:
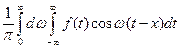 =
= 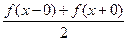 .
.
Формулу Фурье можно переписать в другом виде:
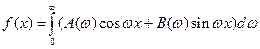 ,
,
где 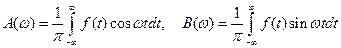 .
.
 2015-04-01
2015-04-01 1043
1043








