Замечание

1).Если функция - четная, то формула Фурье принимает вид 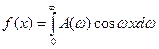, где ;

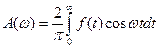в случае нечетной функции - 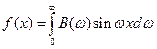, где .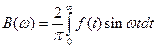

2). Формулу Фурье можно представить в симметричной форме записи, если положить 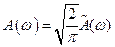, 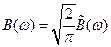. В случае четной функции:

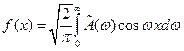, где ;

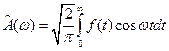в случае нечетной функции:

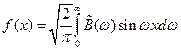, где .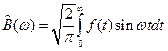

Определение. Функци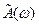и и 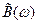называются соответственно косинус – преобразованием и синус – преобразованием Фурье для функции .

Пример. Представить интегралом Фурье функцию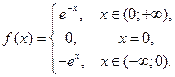

Решение. Функция абсолютно интегрируема на промежутке : .

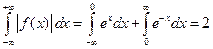Функция нечетная, поэтому находим: .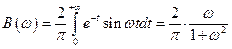

Следовательно, .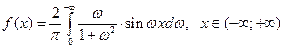

Теория вероятностей

Случайные события и их вероятности