Если функция  четная (т.е.
четная (т.е. 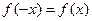 ), то все её коэффициенты
), то все её коэффициенты 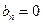 , и ряд Фурье имеет вид
, и ряд Фурье имеет вид
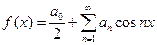 ,
,
где 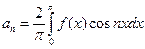 ,
, 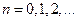 .
.
Если функция  нечетная (т.е.
нечетная (т.е. 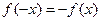 ), то все коэффициенты
), то все коэффициенты 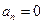 , и её ряд Фурье имеет вид
, и её ряд Фурье имеет вид
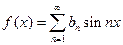 ,
,
где  .
.
Определение. Эти ряды называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Разложение в ряд Фурье функций произвольного периода 2l
Пусть функция  определена на отрезке
определена на отрезке 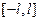 и удовлетворяет на этом отрезке условиям теоремы Дирихле. Введем новую переменную по формуле
и удовлетворяет на этом отрезке условиям теоремы Дирихле. Введем новую переменную по формуле 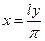 и рассмотрим функцию
и рассмотрим функцию 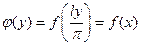 . Функция
. Функция 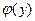 определена на отрезке
определена на отрезке 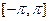 и удовлетворяет теореме Дирихле. Ее ряд Фурье имеет вид:
и удовлетворяет теореме Дирихле. Ее ряд Фурье имеет вид:
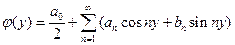 ,
,
где 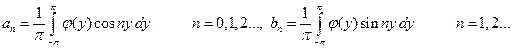 .
.
Вернемся к старой переменной 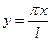 .
.
Определение. Ряд 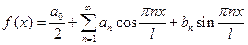
с коэффициентами, вычисляемыми по формулам
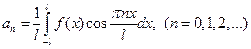 ,
, 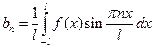 ,
, 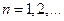
называется рядом Фурье для функции  с периодом
с периодом 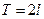 .
.
Замечание. Если  на отрезке
на отрезке 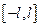 четная, то ее ряд Фурье имеет вид:
четная, то ее ряд Фурье имеет вид: 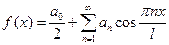 , где
, где 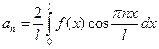 ,
, 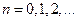 ;
;
Если  - нечетная функция, то
- нечетная функция, то 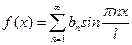 ,
,
где 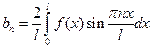 ,
, 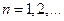 .
.
Пример. Разложить в ряд Фурье 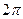 - периодическую функцию, заданную на промежутке
- периодическую функцию, заданную на промежутке 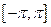 следующим образом:
следующим образом: 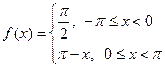 .
.
Решение. Построим график функции  (Рис. 2).
(Рис. 2).
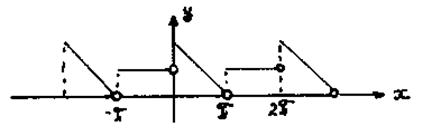
Рис. 2
Данная функция имеет конечное число разрывов первого рода на промежутке 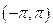 . По теореме Дирихле ее можно разложить в ряд Фурье
. По теореме Дирихле ее можно разложить в ряд Фурье 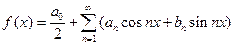 .
.
Вычислим коэффициенты Фурье:
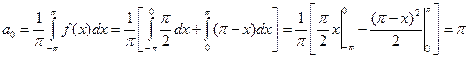 ;
; 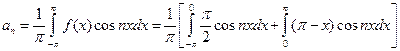 .
.
Ко второму интегралу применим формулу интегрирования по частям:
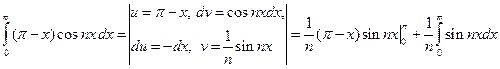 .
.
Тогда 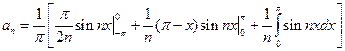 =
= 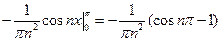 = =
= = 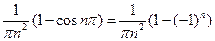 .
.
Коэффициенты с четным индексом обращаются в нуль, а с нечетным, когда 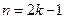 :
: 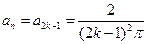 .
.
Определим коэффициенты 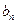 :
:
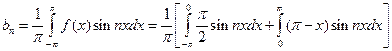 .
.
Проведя вычисления аналогичным образом, получим 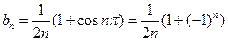 . Из всех коэффициентов
. Из всех коэффициентов 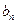 ненулевыми будут коэффициенты с четным индексом
ненулевыми будут коэффициенты с четным индексом 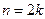 :
: 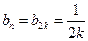 . Поставим найденные коэффициенты в ряд Фурье
. Поставим найденные коэффициенты в ряд Фурье 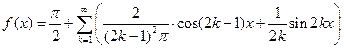 .
.
По теореме Дирихле составленный ряд Фурье сходится к функции 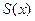 , которая совпадает с
, которая совпадает с  во всех точках ее непрерывности. Поэтому знак
во всех точках ее непрерывности. Поэтому знак  можно заменить знаком равенства:
можно заменить знаком равенства: 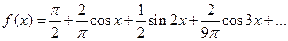 ,
, 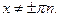
В точках разрыва функции 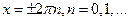 сумма ряда
сумма ряда 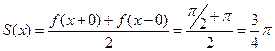 .
.
В точках разрыва 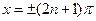 ,
, 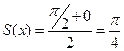 . И так,
. И так,
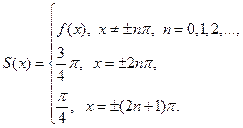
Пример. Разложить в ряд Фурье 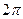 - периодическую функцию, заданную на промежутке
- периодическую функцию, заданную на промежутке 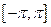 следующим образом:
следующим образом: 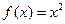 .
.
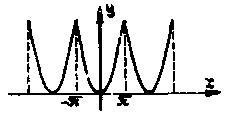 Рис. 3 Рис. 3 |
Решение. График функции изображен на Рис. 3.
Функция  непрерывна на всей оси и может быть разложена в ряд Фурье, сходящийся к ней при всех
непрерывна на всей оси и может быть разложена в ряд Фурье, сходящийся к ней при всех 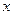 , т.е.
, т.е. 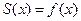 для любого
для любого 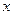 . Так как
. Так как  - четная и
- четная и 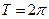 , то
, то 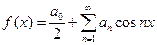 .
.
Вычислим коэффициенты:
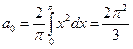 ;
; 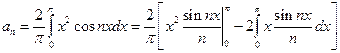 =
= 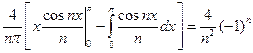 , т.е.
, т.е.
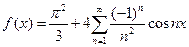 ,
,  .
.
 2015-04-01
2015-04-01 7474
7474
