Теорема 1 (Дирихле). Пусть 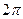 - периодическая функция
- периодическая функция  на отрезке
на отрезке 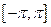 удовлетворяет двум условиям:
удовлетворяет двум условиям:
1)  кусочно – непрерывна (т.е. непрерывна или имеет конечное число точек разрыва 1 рода);
кусочно – непрерывна (т.е. непрерывна или имеет конечное число точек разрыва 1 рода);
2)  кусочно – монотонна (т.е. либо монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна).
кусочно – монотонна (т.е. либо монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна).
Тогда ряд Фурье, соответствующий функции  , сходится на этом отрезке и при этом:
, сходится на этом отрезке и при этом:
- в точках непрерывности функции сумма ряда 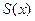 совпадает с самой функцией:
совпадает с самой функцией: 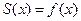 ;
;
- в каждой точке 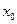 разрыва функции сумма ряда равна:
разрыва функции сумма ряда равна: 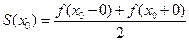 , т.е. равна среднему арифметическому пределов функции
, т.е. равна среднему арифметическому пределов функции  справа и слева;
справа и слева;
- в точках 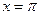 и
и 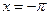 (на концах отрезка) сумма ряда равна
(на концах отрезка) сумма ряда равна 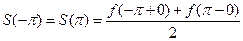 .
.
Таким образом, если 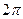 - периодическая функция
- периодическая функция  непрерывна на отрезке
непрерывна на отрезке 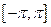 , то имеет место разложение:
, то имеет место разложение: 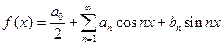 .
.
 2015-04-01
2015-04-01 1636
1636








