2015-04-01
475
Цель: формирование умения выполнять основные операции над векторами в координатах.
Задание для самостоятельной внеаудиторной работы:
& 8.1.Выучите определение свободного вектора, координат вектора на плоскости. Пользуясь обобщающей таблицей, проанализируйте, какие операции над векторами в координатах выполнимы, в чем заключаются признаки коллинеарности и перпендикулярности векторов.
i8.2. В треугольнике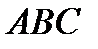 
вершины имеют координаты 
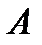(2; -1), 
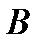(5; -5), 
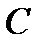(8; -5). Найдите:
1) координаты вектора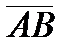 
;
2) длину стороны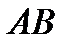 
;
3) координату точки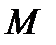 
- середины отрезка 
;
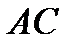4) длину медианы 
;
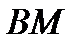5) координаты вектора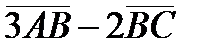 
;
6) косинус угла между векторам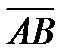и 
и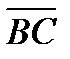 
;
¶7) треугольник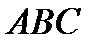 
достроили до параллелограмма 
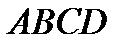; найдите координату вершины 
.
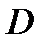Решив задания 1 - 6 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, какой профессии были отданы три года жизни создателя аналитической геометрии Рене Декарта (1596-1650).
Профессия:
Карта ответов:
| Е | И | Й | Н | О | Р | У | Ф | Ц | Ч | Ы |
| (3;-12) | (5;-3) | (-3;4) | (3;-4) | 0,6 |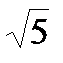 
| (10;-6) | -0,2 |
?8.3. При каком значении т векторы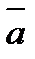 
= (-4; 1) и 
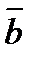=(т; -2)
а) взаимно перпендикулярны; б) коллинеарны.
?8.4. Докажите, что 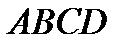, где 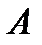(-2; 1), 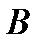(1; 2), 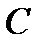(4; -1), 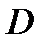(-2; -3) – трапеция с основаниям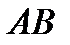и 
и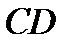 
. Определите, является ли трапеция равнобокой. На оси ОХ найдите координаты точки, равноудаленной от точек А и В.
¶8.5. В прямоугольном треугольнике АВС угол С равен 90о. Найдите координаты точки С, если её абсцисса равна -1, В (3; 0), А (-4; 1).
Методические указания по выполнению работы:
Вектор – это направленный отрезок. Все равные между собой направленные отрезки называют свободным вектором.
Коэффициенты (x; y) разложения вектора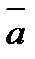 
по векторам 
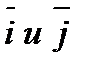(единичным взаимно перпендикулярным векторам)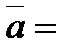 
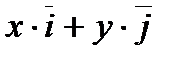называют координатами вектора на плоскости.
При решении задач по теме «Векторы» используйте следующие рекомендации:
- Выпишите исходные данные – дано. Если в условии задачи сказано о коллинеарности, перпендикулярности, равенстве длин векторов, то это также необходимо выписать.
- Определите, что нужно найти или что доказать в соответствии с условием задачи.
- Опираясь на то, что нужно найти, попытайтесь поискать ключ к решению: выбрать в таблице нужные операции или использовать признаки коллинеарности и перпендикулярности векторов, сформулированные в теоремах 1 и 2.
