2015-04-01
1165
| № | Вид операции | Исходные данные | Операции в координатах |
| Координаты вектора | А (х1; у1); В (х2;у2) |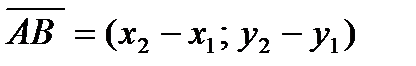 
| |
| Длина вектора |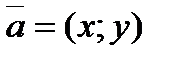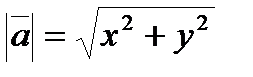 
| 
| |
| Сложение и вычитание векторов |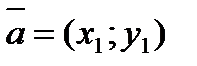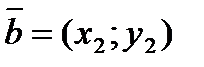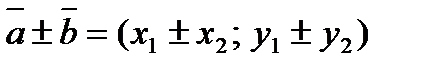  
| 
| |
| Умножение вектора на число |  ;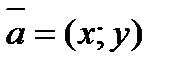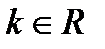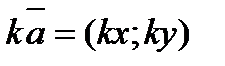 
| 
| |
| Скалярное произведение векторов |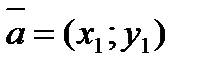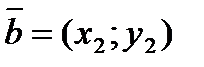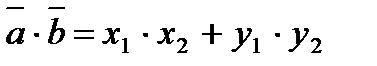  
| 
| |
| Угол между векторами |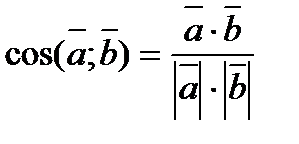 
| ||
| Координаты середины отрезка | А (х1; у1); В (х2;у2) |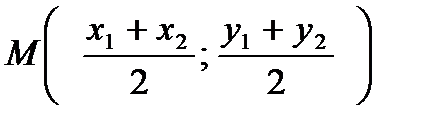 
| |
| Расстояние между точками | А (х1; у1); В (х2;у2) |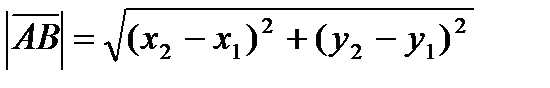 
|
Теорема 1. Если векторы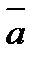 
и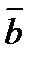 
коллинеарны, то их соответствующие координаты пропорциональны:
если 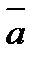= (х1; у1) и 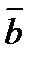= (х2; у2) коллинеарны, то 
.
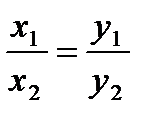Теорема 2. Если ненулевые векторы 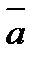и 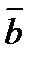взаимно перпендикулярны, то их скалярное произведение равно нулю, и наоборот, если скалярное произведение векторов равно нулю, то векторы перпендикулярны: 
(
) 
.
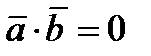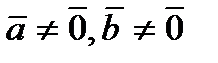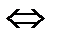
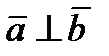Пример 1. Даны точки А (4;-3), В (-2;-9).
Найти: 1) координаты вектора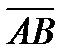 
;
2) длину вектора ;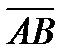
3) координаты точки М – середины АВ.
Решение:
1) Воспользуемся формулой нахождения координат вектора: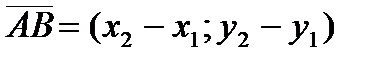 
.
Тогда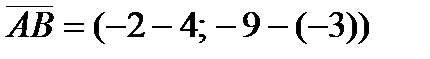 
; 
.
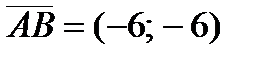2) Зная координаты вектора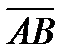 
, найдем его длину по формуле: 
.
.
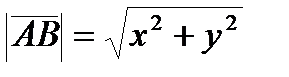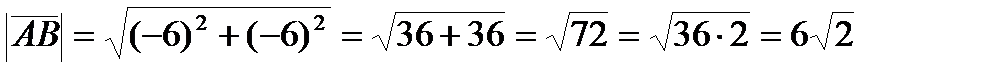3) Пусть точка М – середина отрезка АВ. Тогда ее координаты находятся по формуле: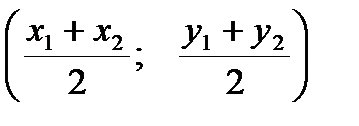 
: М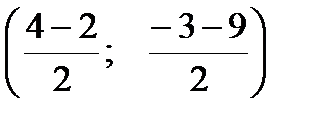 
; М (1; -6).
Ответ: 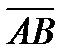=(-6; -6), 
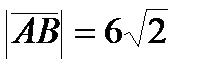, М (1; -6).
| ^ |
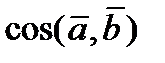Пример 2. Даны 
, 
.
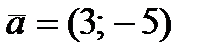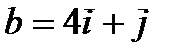Найдите: 1)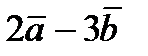 
; 2) 
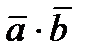; 3)
Решение:
1) Вектор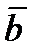 
задан в виде разложения по базисным векторам 
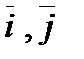. Его координаты находятся как коэффициенты разложения вектора по базису: 
.
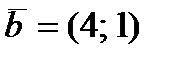Найдем координаты векторов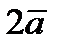 
и 
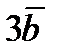по формуле: 
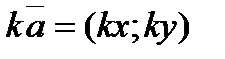. Тогда
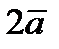= (6; -10); 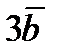= (12; 3).
Воспользуемся формулой нахождения суммы и разности векторов: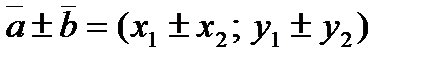 
. Получим, что 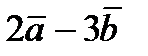= (6-12; -10-3); 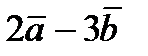= (-6; -13).
2) Воспользуемся формулой нахождения скалярного произведения векторов: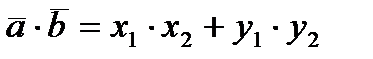 
.
Получим: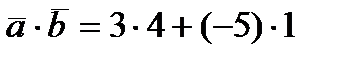 
;
; 
.
| ^ |
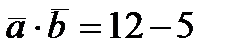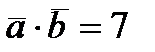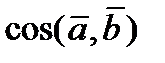3) Найдем косинус угла между векторами по формуле = 
.
;
| ^ |
;
= 
| ^ |
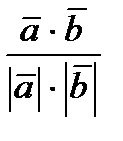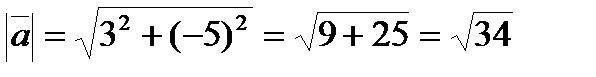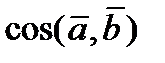
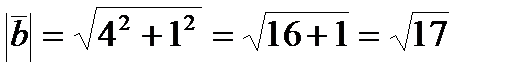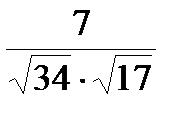
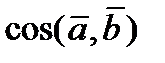Ответ: 1) 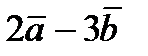= (-6; -13); 2) 
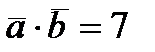; 3) = 
.
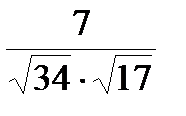Пример 3. При каком значении n векторы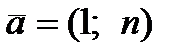 
, 
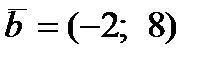
1) коллинеарны; 2) перпендикулярны?
Решение:
1) Воспользуемся теоремой 1: если векторы коллинеарны, то их соответствующие координаты пропорциональны. Получим, что
; 
.
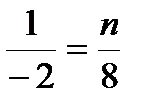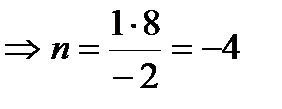Следовательно, при n = – 4 векторы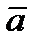 
и 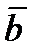коллинеарны.
2) Воспользуемся теоремой 2: если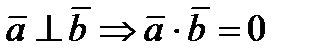 
.
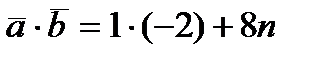Þ –2 + 8 n = 0; 8 n = 2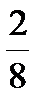; n = 
; n =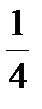 
; n = 0,25.
Следовательно, при n = 0,25 векторы 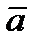и 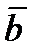перпендикулярны.
Ответ: 1) n = – 4; 2) n = 0,25.
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2012. – 320с. – Глава 3, §3.1, 3.2, стр. 53 – 60.
2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 2, § 8 – 10, стр. 63 – 73.
3. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 3, §1 - 4, стр. 125 - 141.
