2015-04-01
692
Цель: формирование умения составлять уравнения прямых на плоскости.
Задание для самостоятельной внеаудиторной работы:
& 9.1.Опираясь на обобщающие таблицы, изучите, какими способами можно задать прямую, и какие виды уравнения прямой существуют.
?9.2. В треугольнике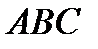 
заданы координаты вершин 
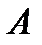(-5; 3), 
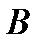(2; -1), 
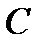(6; 3). Составьте уравнение:
а) прямой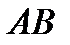 
;
б) медианы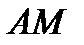 
;
в) прямой, проходящей через точку 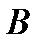параллельно 
;
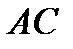г) прямой, проходящей через точку 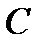с угловым коэффициентом 
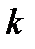=3.
?9.3.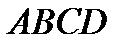 
- трапеция с основаниям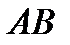и и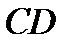 
, в которой 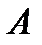(-2; 1), 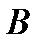(1; 2), 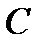(4; -1), 
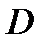(-2; -3).
Составьте уравнение:
а) диагонали 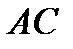в каноническом виде;
б) прямой, параллельной основаниям, проходящей через точку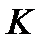 
(-3; -1) в параметрическом виде;
в) прямой, проходящей через точку 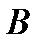и образующей с положительным направлением оси 
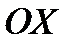угол 
(вид уравнения прямой – с угловым коэффициентом);
г) средней линии трапеции в каноническом виде;
д) прямой, проходящей через точку 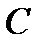параллельно прямой 
.
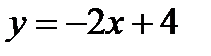¶9.4. Запишите уравнение прямой во всех видах (общем, каноническом, параметрическом, с угловым коэффициентом) и постройте эту прямую:
а)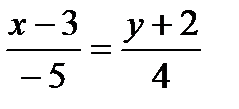 
; б)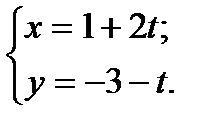 
Методические указания по выполнению работы:
Уравнением линии на плоскости называется уравнение с двумя переменными x и y, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Прямые – самые простые линии на плоскости. Им соответствуют уравнения первой степени.
При решении задач удобно использовать следующие обобщающие таблицы:
