Дискретизация непрерывного сигнала

Замена непрерывного сигнала совокупностью выборок (без потери информации) основана на теореме отсчетов (теорема Котельникова): если наивысшая частота в спектре оригинала s(t) меньше чем частота дискретизации F_m, то сигнал s(t) полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга не более чем на 1 /2F_m сек.

В соответствии с этой теоремой сигнал s(t), ограниченный по спектру наивысшей частотой 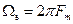, может быть представлен рядом

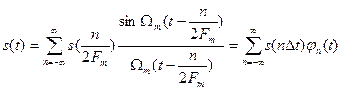. (1.3)

В этом выражении l/2F_m =∆t обозначает интервал между двумя отсчетными, a s(n/2F_m) = s(n ∆ t) — выборки функции s(t) в моменты времени t= n∆t.

Представление заданной функции s(t) рядом (1.3) иллюстрируется рис. 1.8

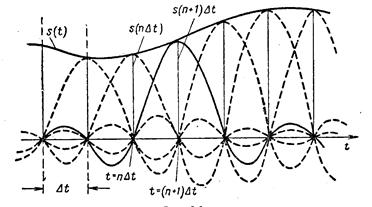
Рис.1.8. Представление сигнала в виде ряда Котельникова

Функция вида

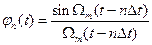(1.4)

обладает следующими свойствами:

• в точке t = n∆t φ _n(n ∆t) = 1, а в точках t = k, где k — любое целое, положительное или отрицательное число, отличное от п, φ _n(k∆t) = 0;
• спектральная плотность функции φ ₀(t) равномерна в полосе частот 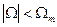и равна 1/2F_m =π/Ω_m. Так как функция φ _n(t) отличается от φ ₀(t) только сдвигом на оси времени на величину n∆t, то спектральная плотность функции φ _n(t).

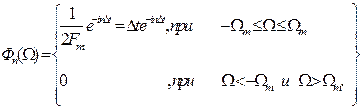. (1.5)

Модуль этой функции изображен на нижней части рис.1.9 (сплошной линией).

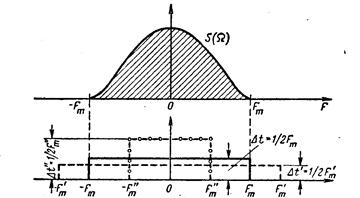
Рис.1.9 Связь между спектром сигнала s(t) и спектром функции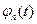

Ряд (1.3) точно определяет заданный сигнал s(t) в точках отсчета, поскольку коэффициентами ряда являются сами выборки из функции, т. е. величины s(n∆t). Можно доказать, что ряд (1.3) определяет функцию s(t) влюбой момент t, а не только в точках отсчета t =n∆t. Воспользуемся для этого общими правилами разложения функции по ортогональной системе. В данном случае разложение производится по функциям вида (1.4), для которых интервал ортогональности равен бесконечности, а норма ||φ_n||:

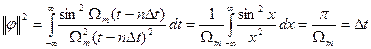. (1.6)

Применим для определения значений коэффициентов ряда общую формулу, справедливую для обобщенного ряда Фурье:

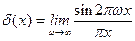. (1.7)

Сам обобщенный ряд Фурье представлен коэффициентами:

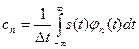. (1.8)

При этом исходим из условия, что s(t) — квадратично интегрируемая функция (энергия сигнала конечна).

Для вычисления интеграла в выражении (1.8) воспользуемся формулой, согласно которой

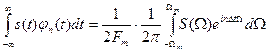. (1.9)

Пределы интегрирования здесь приведены в соответствие с заданной граничной частотой 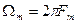в спектре сигнала s(0), а также в спектре функции φ _n(t).

Интеграл в правой части (1.9) с коэффициентом 1/2π есть не что иное, как значение s(t) в момент t = n∆t. Таким образом,

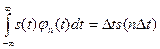. (1.10)

Подставляя этот результат в (1.8), получаем окончательное выражение

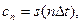(1.11)

из которого следует, что коэффициентами ряда (1.3) являются выборки функции s(t) в точках t = n∆t.

Поскольку ограничение спектра конечной наивысшей частотой обеспечивает непрерывность функции s(t), ряд (1.3) сходится к функции s(t) при любом значении t.

Если взять интервал между выборками ∆t' меньшим, чем ∆t=1/ 2F_m, то ширина 2F'_m спектра Ф'_n(Ω) функции φ '_n(t) будет больше, чем у спектра S(Ω) сигнала s(t) (рис. 1.8), но это не отразится на величине коэффициентов с_п. Модуль функции Ф'_n(Ω) изображен на рис.1.8 пунктиром.

При увеличении же ∆t'' по сравнению с ∆t спектр Ф''_n(Ω) функции φ ''_n(t) (на рис. 1.8 показан штрих-пунктиром) становится уже, чем спектр сигнала s(t), и при вычислении интеграла в выражении (1.9) пределы интегрирования должны быть (-2πF''_m, 2πF''_m) вместо (-2πF_m, 2πF_m). Коэффициенты с_n при этом являются уже выборками не задан­ного сигнала s(t), а некоторой другой функции s₁(t), спектр которой ограничен наивысшей частотой F''_m.

Итак, сокращение интервалов между выборками по сравнению с величиной 1/2F_m допустимо, но бесполезно. Увеличение же интервала сверх величины 1/2F_m недопустимо.

Рассмотрим теперь случай, когда длительность сигнала s(t) конечна и равна Т, а полоса частот по-прежнему равна F_m. Эти условия, строго говоря, несовместимы, так как функция конечной длительности обладает теоретически бесконечно широким спектром. Практически, однако, всегда можно определить наивысшую частоту спектра F_m так, чтобы «хвосты» функции времени, обусловленные отсеканием ча­стот, превышающих F_m, содержали пренебрежимо малую долю энер­гии по сравнению с энергией заданного сигнала s(t). При таком допущении, если имеется сигнал длительностью Т с полосой частот F_m, общее число независимых параметров т. е. значений s(n∆t), которое необходимо для полного задания сигнала, очевидно, равно

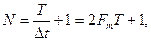(1.12)

при 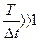можно считать N = 2F_mT. При этом выражение (1.3) принимает следующий вид:

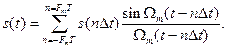(1.13)

Число N иногда называют числом степеней свободы сигнала s(t) так как даже при произвольном выборе значений s(n∆t) сумма вида (1.13) определяет функцию, удовлетворяющую условиям заданного спектра и заданной длительности сигнала. Число N иногда называют также базой сигнала.

В ряде случаев встречается необходимость представления сигнала с помощью частотных выборок спектральной функции S(Ω), а не вре­менных выборок функции s(t). Для функции S(Ω) можно составить ряд, аналогичный выражению (1.3). Это нетрудно сделать на основании взаимной заменимости переменных t и Ω в преобразованиях Фурье. Применительно к выражению (1.3) это означает, что t должно быть заменено на Ω, 2Ω_m на Т, 2F_m на Т/2π; ∆t = 1/2F_т на ∆Ω = 2π /Т. Таким образом получается

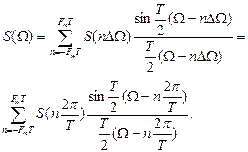(1.14)

Если ранее временной интервал между двумя соседними выбор­ками должен был не превышать 2π/2Ω_m,то теперь частотный интервал не должен превышать 2π/Т. При ширине спектра 2 Ω_m, охватывающей область частот - Ω_m < Ω < Ω_m, число выборок равно 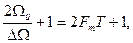как и при представлении сигнала рядом (1).

В общем случае выборки 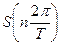являются комплексными числами и в каждой отсчетной точке на оси частот должны быть заданы два параметра — действительная и мнимая части 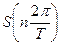(или модуль и аргумент). Таким образом, общее число параметров получается вдвое большим, чем при временном представлении сигнала, когда вы­борки 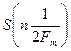— действительные числа. 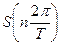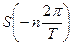Избыточность представления сигнала в частотной области легко устраняется, если учесть, что и являются комплексно-сопряженными числами, так что задание одной из них однозначно определяет другую. Таким об­разом, число независимых параметров или степеней свободы сигнала равно 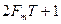, как и при представлении сигнала во временной области.

Энергию и среднюю мощность сигнала нетрудно выразить через заданную последовательность временных выборок.

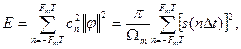(1.15)

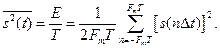(1.16)

Из последнего выражения видно, что средняя за время Т мощность непрерывного сигнала равна среднему квадрату выборки. Усреднение производится по всем отсчетным точкам, число которых равно 2F_mТ.