2015-04-01
418
Пусть имеются выборочные наблюдения над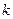 
переменными 
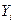и 
, 
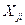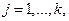
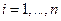, где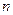 
- количество наблюдений:
| … | 
| … |
| ||
| 
| … |
| … | 
|
| 
| … | 
| … | 
|
| … | … | … | … | … | … |
| 
| … | 
| 
|
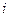
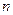
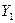
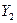
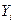
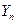
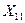
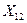
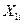
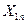
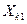
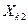
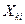
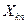
Предположим, что существует линейное соотношение между результирующей переменно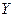й 
и 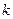объясняющими переменными 
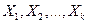. Тогда с учетом случайной ошибки 
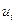запишем уравнение:
, 
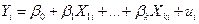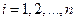(3.1)
В (3.1) неизвестны коэффициенты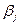 
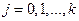и параметры распределения 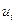. Задача состоит в оценивании этих неизвестных величин. Модель (3.1) называется классической линейной моделью множественной регрессии (КЛММР). Часто имеют в виду, что переменная 
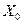при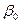 
равна единице для всех наблюдений .
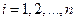Относительно переменных модели в уравнении (3.1) примем следующие основные гипотезы:
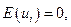
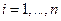. (3.2)
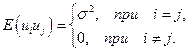(3.3)
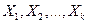- неслучайные величины. (3.4)
Не должно существовать строгой
линейной зависимости между переменными 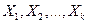(3.5)
Первая гипотеза (3.2) означает, что переменные 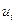имеют нулевую среднюю.
Суть гипотезы (3.3) состоит в том, что все случайные ошибки 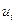имеют постоянную дисперсию, т.е. выполняется так называемое условие гомоскедастичности дисперсии.
Согласно (3.4) в повторяющихся выборочных наблюдениях источником возмущений 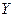являются случайные колебания 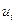, а значит, свойства оценок и критериев обусловлены объясняющими переменными .
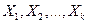Последняя гипотеза (3.5) означает, в частности, что не существует линейной зависимости между объясняющими переменными, включая переменную 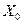, которая всегда равна 1.
Условия (3.2)-(3.4) аналогичны соответствующим условиям для случая двух переменных п.2.2.
