1. Определите свойства соответствий между множествами 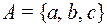 и
и 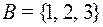 . Какие из них являются функциями типа
. Какие из них являются функциями типа 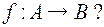
1) 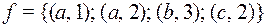 ; 3)
; 3) 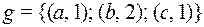 ;
;
2) 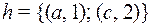 ; 4)
; 4) 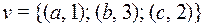 .
.
2. Соответствие задано рисунком. Определить свойства соответствия. Является ли оно функцией, отображением?
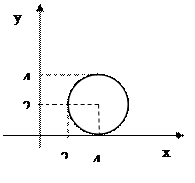
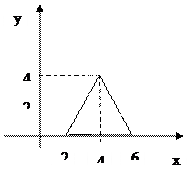
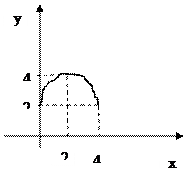
Рис 1. Рис.2. Рис.3.
Для рис. 1 определить:
1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (2; 4]; 5) прообраз 2; 6) прообраз 4; 7) прообраз [2;4]; 8) прообраз (0;4).
Для рис. 2 определить:
1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (4; 6]; 5) прообраз 0; 6) прообраз 4; 7) прообраз [0;4]; 8) прообраз (0;4).
Для рис. 1 определить:
1) образ 2; 2) образ 4; 3) образ [2; 4]; 4) образ (0; 4]; 5) прообраз 2; 6) прообраз 4; 7) прообраз [2;4]; 8) прообраз (2;4).
3. Определите свойства соответствий между множествами 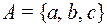 и
и 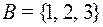 . Какие из них являются функциями типа
. Какие из них являются функциями типа 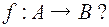
1) 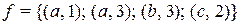 ; 3)
; 3) 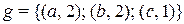 ;
;
2) 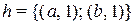 ; 4)
; 4) 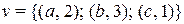 .
.
4. Определите, какие из следующих подмножеств 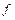 множества
множества 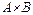 являются функциями
являются функциями 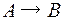 . Объясните свой ответ.
. Объясните свой ответ.
1) 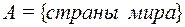 ,
, 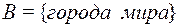 ,
,
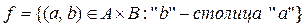
2) 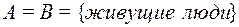 ,
,
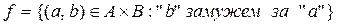
5. Пусть 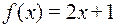 ,
, 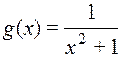 – функции
– функции 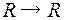 . Найдите:
. Найдите:
1) 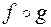 ; ;
| 3) 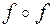 ; ;
| |
2) 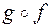 ; ;
| 4) 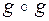 . .
|
6. Дано множество 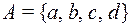 и два преобразования этого множества (т.е. функции типа
и два преобразования этого множества (т.е. функции типа 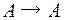 ):
):
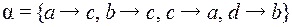 и
и 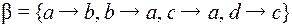
или, как обычно принято записывать преобразования конечных множеств:
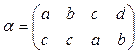 и
и 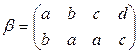 .
.
Найти композиции преобразований: 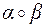 и
и 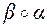 .
.
7. Найти композиции преобразований: 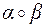 и
и 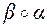 , если
, если
1) 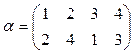 и
и 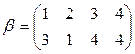 ;
;
2) 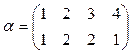 и
и 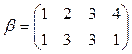 ;
;
3) 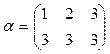 и
и 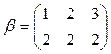 .
.
8. Пусть тип функции 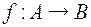 .Для различных А, В и f определить область определения и область значения. Будут ли у этих функций обратные? Если да, то будут ли они отображениями. Сделайте вывод о том, какими свойствами должна в этом случае обладать функция.
.Для различных А, В и f определить область определения и область значения. Будут ли у этих функций обратные? Если да, то будут ли они отображениями. Сделайте вывод о том, какими свойствами должна в этом случае обладать функция.
1) 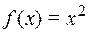 , если а) А=R; В=R; б) A=N; В=N.
, если а) А=R; В=R; б) A=N; В=N.
2) 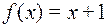 , если а) А=R+; В=R; б) A=N0; В=N.
, если а) А=R+; В=R; б) A=N0; В=N.
3) 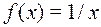 , если а) А=R; В=R; б) A=R+; В=R.
, если а) А=R; В=R; б) A=R+; В=R.
4) 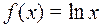 , если а) А=R; В=R; б) A=R+; В=R+.
, если а) А=R; В=R; б) A=R+; В=R+.
5) 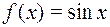 , если а) А=R; В=R;
, если а) А=R; В=R;
б) A= 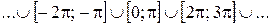 ; В= [0; 1].
; В= [0; 1].
9. Определить область определения и область значений композиций 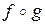 и
и 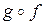 .
.
1) 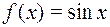 ;
; 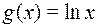 ; г)
; г) 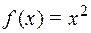 ;
; 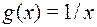 ;
;
2) 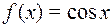 ;
; 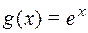 ; д)
; д) 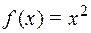 ;
; 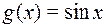 ;
;
3) 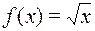 ;
; 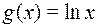 ; е)
; е) 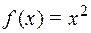 ;
; 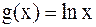 .
.
10. Найти композиции преобразований: 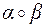 и
и 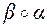 , если
, если
1) 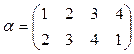 и
и 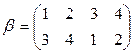 ;
;
2) 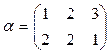 и
и 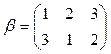 ;
;
3) 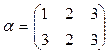 и
и 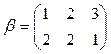 .
.
11. Найти композиции 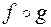 ,
, 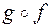 ,
, 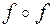 и
и 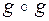 , если
, если 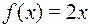 и
и 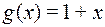 - функции типа
- функции типа 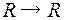 .
.
1) 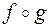 =
= 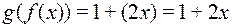 ;
;
2) 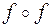 =
= 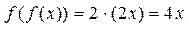 ;
;
3) 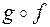 =
= 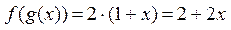 ;
;
4) 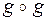 =
= 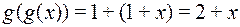 .
.
 2015-04-01
2015-04-01 532
532








