Теорема (о числе подмножеств конечного множества)

Если для конечного множества А (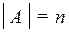), то число всех подмножеств множества А равно .

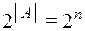Множества равномощны, если между их элементами можно установить взаимно однозначное соответствие.

Счетные множества это множества равномощные N (т. е. между ними и N можно установить взаимно однозначное соответствие).

Утверждение 1: Множество 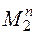– счетно.

Утверждение 2: Любое бесконечное подмножество множества N – счетно.

Утверждение 3: Множество 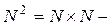– счетно.

Следствие: Множество 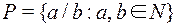– положительных рациональных чисел – счетно.

Утверждение 4: Множество 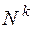, где 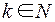, - счетно.

Утверждение 5: Объединение конечного числа счетных множеств 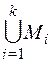– счетно.

Утверждение 6: Объединение счетного множества конечных множеств – счетно.

Следствие: Множество всех слов конечного алфавита – счетно.

Утверждение 7: Объединение счетного множества счетных множеств 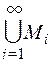– счетно.

Несчетные бесконечные множества называются множествами мощности континуум. (Мощность несчетного бесконечного множества называется континуумом).

Теорема (Кантора): Множество всех действительных чисел отрезка [0, 1] имеет мощность континуума.

Следствие: Множество всех подмножеств несчетного множества континуально.