§1. Понятия множества и соответствия между множествами.
Если каждому элементу множества А поставлен в соответствие единственный элемент множества В, то соответствие между множествами А и В называется функцией.
Множество А – область определения функции; множество В – область значений функций.
Пусть х – элемент множества А; у – элемент множества В; ƒ – закон соответствия; тогда можно записать: у=ƒ(х).
Существуют различные способы задания функции: табличный, графический, аналитический.
Числовая функция ƒ, определенная на множестве всех натуральных чисел, называется бесконечной числовой последовательностью.
Рассмотрим последовательность 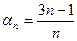
С возрастанием номера п член последовательности сколько угодно близко приближаются к числу 3; например, 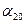 =
= 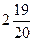 ;
; 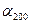 =
= 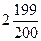 и т.д.
и т.д.
Поставим такой вопрос: каким должно быть число п, чтобы модуль разности | 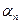 - 3 | был меньше 0,001? Для этого решим неравенство |
- 3 | был меньше 0,001? Для этого решим неравенство | 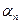 - 3|< 0,001.
- 3|< 0,001.
Имеем 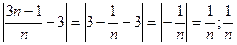 <0,001; n>N=1000.
<0,001; n>N=1000.
Для любого положительного числа 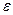 неравенство |
неравенство | 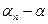 | равносильно равенству
| равносильно равенству 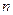 >
> 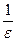 , т.е.
, т.е. 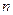 >N =
>N = 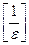 , где
, где 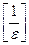 – целая часть числа.
– целая часть числа.
Число 3 является пределом рассмотренной последовательности.
§2. Определение предела последовательности, предел функции.
 Число а называется пределом последовательности (
Число а называется пределом последовательности (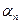 ), если для любого положительного числа
), если для любого положительного числа 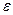 найдется такое натуральное число N, что для всех
найдется такое натуральное число N, что для всех 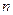 >N выполняется равенство |
>N выполняется равенство | 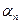 -
- 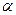 |<
|< 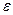 ;
; 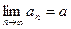

При вычислении пределов функции используются следующие теоремы:
- Предел постоянной величины равен этой величине:
limc=c
- Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:
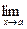 (ƒ
(ƒ 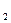
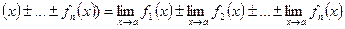
3. Предел произведение конечного числа функций равен произведению
пределов этих функций, если существуют конечные пределы сомножителей.
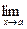 (ƒ
(ƒ 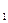
4. Предел частного двух функций равен частному пределов этих функций, если предел делителя отличен от нуля и пределы делимого и делителя существуют:
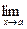
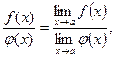 если
если 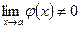
5. Постоянный множитель можно выносить за знак предела т.е.
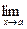 (c
(c 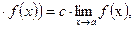 где с=const
где с=const 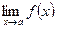 существует.
существует.
6. Если функция f(х) удовлетворяет неравенству
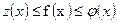 и если
и если 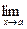
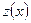 =b.
=b. 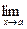 = b, то
= b, то 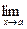 f(х)= b
f(х)= b
З а м е ч а н и е. Функция f(x) может иметь только один предел при х,
стремящемся к а.
Приступим к отысканию пределов функций.
При вычислении предела функции необходимо указать предел аргумента.
Пример 1. Вычислить 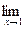 (4x
(4x 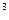 -2x
-2x 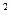 -3).
-3).
Р е ш е н и е. Применяя теоремы 1, 2, 3 и 5, получим
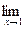 (4x
(4x 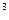 -2x
-2x 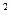 -3) = 4(
-3) = 4(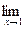 x)
x) 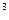 -2(
-2(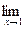 х)
х) 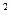 - 3=4
- 3=4 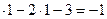

Пример 2. Вычислить 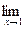 (x
(x 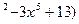
Р е ш е н и е.

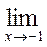 (x
(x 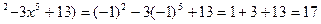
Пример 3. Вычислить 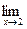
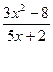
Р е ш е н и е. Так как lim (5x+2) 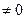 , то используя теорему 4, находим:
, то используя теорему 4, находим:
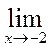

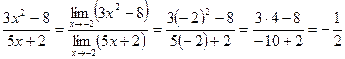
Пример 4. Вычислить 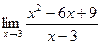
Р е ш е н и е. Здесь теорема о пределе частного неприменима, так как
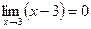 .Упростим числитель дроби, используя формулу сокращенного
.Упростим числитель дроби, используя формулу сокращенного
умножения, и сократим дробь на общий множитель
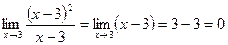

Пример 5. Вычислить 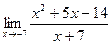
Р е ш е н и е. Теорема о пределе частного неприменима, так как 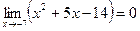 и
и 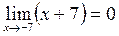 . Квадратный трехчлен в числителе дроби разложим на множители и сократим дробь на общий множитель.
. Квадратный трехчлен в числителе дроби разложим на множители и сократим дробь на общий множитель.
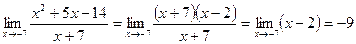
Пример 6. Вычислить 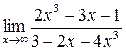
Р е ш е н и е. Чтобы избавиться от неопределенности, разделим числитель и знаменатель дроби на 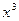 (имеем дело с неопределенностью вида
(имеем дело с неопределенностью вида 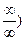 :
:

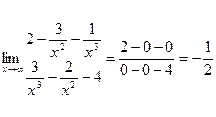

Пример 7. Вычислить 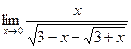
Р е ш е н и е. При вычислении предела имеем неопределенность 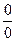 . Чтобы избавиться от неопределенности, умножим числитель и знаменатель на сопряженный знаменателю множитель
. Чтобы избавиться от неопределенности, умножим числитель и знаменатель на сопряженный знаменателю множитель 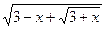 и затем сократим дробь:
и затем сократим дробь: 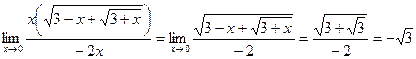
Пример 8. Вычислить 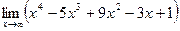
Р е ш е н и е. Для вычисления этого предела под знаком предела выносим х 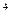 за скобку, при этом получим:
за скобку, при этом получим:
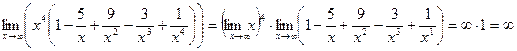
(При х 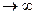 величины
величины 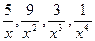 бесконечно малые и их пределы равны нулю).
бесконечно малые и их пределы равны нулю).
- Дайте определение функции, области определения функции.
- Укажите способы задания функции.
- Что называется пределом функции.
- Сформулируйте теоремы о пределах.
 2015-04-01
2015-04-01 2300
2300
