§1.Неопределенный интеграл, его свойства. Правила и формулы дифференцирования. Непосредственное дифференцирование.
Основная задача интегрального исчисления обратна основной задаче дифференциального исчисления.
Пусть дана функция f (x). Требуется найти такую функцию F (x), что dF(x)=f ' (x) dx, т.е. F' (x)= f (x).
Функция F(x) называется первообразной для функции f (x). Выражение
F(x) +C, где С – произвольная постоянная, представляет совокупность всех первообразных для функции f (x) и называется неопределенным интегралом. Действие нахождения функции по её дифференциалу называется интегрированием.
Необходимо выучить основные свойства неопределенного интеграла и основные формулы интегрирования (табличные интегралы).
Приведем основные свойства неопределенного интеграла:
- Действия интегрирования и дифференцирования являются взаимно обратными:
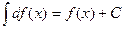 (в частном случае
(в частном случае 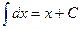 ;
; 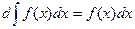 ;)
;) 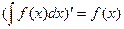 .
. - Постоянный множитель подынтегрального выражения можно вывести за знак интеграла:
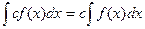 , где с =const
, где с =const
- Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от каждой функции в отдельности (и наоборот).
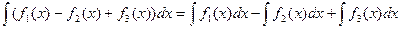 .
.
Основные формулы интегрирования:
(1) 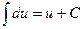 (2)
(2) 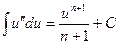 , где n
, где n 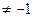
(3) 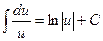 (4)
(4) 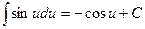
(5) 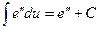 (6)
(6) 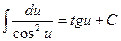
(7) 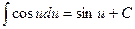 (8)
(8) 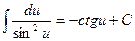
Пример 1. Найти 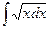
Р е ш е н и е. Воспользуемся определением степени с дробным показателем и найдем интеграл
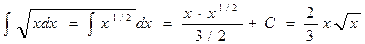
Пример 2. Найти: а) 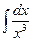 ; б)
; б) 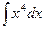
Р е ш е н и е. а) Воспользуемся определением степени с отрицательными показателями и найти интеграл
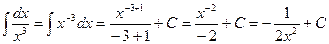
б) По формуле (2) найдем интеграл
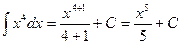
Пример 3. Найти: 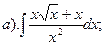
а) В подынтегральном выражении разделим числитель на
знаменатель и воспользуемся свойством неопределенного интеграла. 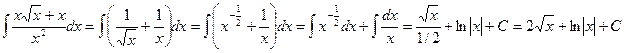 .
.
Неопределенные интегралы вычислены с использованием формул (2) и (3) таблицы интегралов.
Пример 4. Вычислить I = 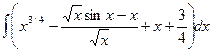
Р е ш е н и е. Выполним элементарные преобразования над подынтегральной функцией:
I = 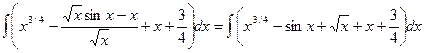
Используя свойство 3 неопределенного интеграла, получим
I = 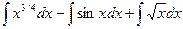 +
+ 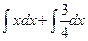
Далее, используем табличные формулы (2) и (6), а также свойство 2 неопределенного интеграла:
I 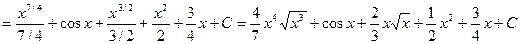
Интегрирование подстановкой. Приём интегрирования функции, при котором путем замены всей подынтегральной функции или какой либо её части новым переменным приводится данный интеграл к табличному, называется интегрированием подстановкой.
Пример 5. Вычислить 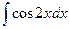
Р е ш е н и е. Выполним замену 2 х = t; тогда дифференцируя левую и правую части равенства, получим 2 dx = dt и dx = 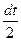
Следовательно,
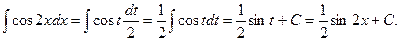
При решении мы вынесли за знак интеграла сомножитель 1/2, применили формулу (7) и вернулись к прежней переменной х.
Пример 6. Вычислить 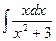 .
.
Р е ш е н и е. Воспользуемся подстановкой х 2 + 3 = t, где t – новая переменная. Продифференцируем обе части равенства:
2xdx = dt, т.е. xdx= 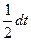 . Тогда интеграл имеет вид:
. Тогда интеграл имеет вид:
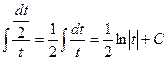 .
.
Произведя замену t = х 2 + 3, получим
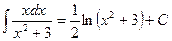
Пример 7. Найти 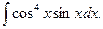
Р е ш е н и е. Замечаем, что sin xdx есть дифференциал функции – cos x. Полагая cos x =z, находим - sin xbх = bz, т.е. sin xbх = bz. Тогда интеграл имеет вид
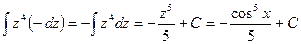
Пример 8. Вычислить 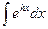
Р е ш е н и е. Положим kх = t, тогда k · dx = dt, значит, dx= 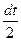
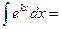
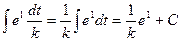
Методом подстановки или методом элементарных преобразований были получены следующие табличные интегралы:
(10) 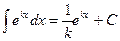 (11)
(11) 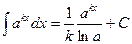
(12) 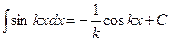 (13)
(13) 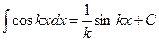
(14) 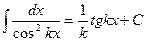 (15)
(15) 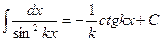
§2. Определенный интеграл, его свойства. Формула Ньютона- Лейбница.
Пусть функция у = f (x) разделена на отрезке от а до b на n элементарных равных частей точками a = x0 < x1 < x2 < …< xn = b; выберем на каждом отрезке от х 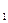 -1 до
-1 до 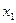 произвольную точку
произвольную точку 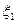 и обозначим через
и обозначим через 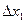 длину каждого такого отрезка.
длину каждого такого отрезка.
Интегральной суммой для функции 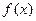 на отрезке от a до b называется сумма вида:
на отрезке от a до b называется сумма вида:
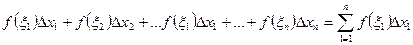 .
.
Определенным интегралом от функции f (x) на отрезке от a до b называется пределинтегральной суммы при условии, что длина элементарного отрезка стремится к нулю; при этом употребляется запись 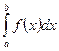 .
.
Числа a и b называются нижним и верхним пределами интегрирования.
Таким образом,
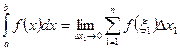 .
.
Для любой функции f (x), непрерывной на отрезке от a до b, всегда существует определенный интеграл 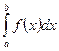 .
.
Основными свойствами определенного интеграла являются:
- Постоянный множитель можно выносить за знак определенного интеграла:
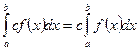
- Определенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждого слагаемого в отдельности:
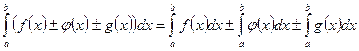
- При перемене местами верхнего и нижнего пределов интегрирования меняется знак определенного интеграла на противоположный:
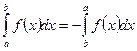
- Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
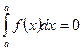
Для вычисления определенного интеграла от функции f (x) в том случае, когда можно найти соответствующий определенный интеграл, служит формула Ньютона-Лейбница:
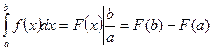
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Все методы интегрирования рассматриваемые при изучении неопределенного интеграла, используются при вычислении определенного интеграла. Отметим, что если определенный интеграл вычисляется методом подстановки, то при переходе к новой переменной необходимо изменить и пределы интегрирования.
Пример 9. Вычислить 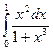
Р е ш е н и е. Положим 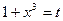 , тогда
, тогда 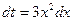 , т.е.
, т.е.
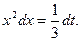 Если х =1, то t =2; если х =0, то t =1. Значит,
Если х =1, то t =2; если х =0, то t =1. Значит,
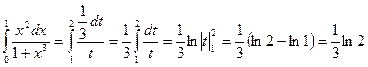
Пример 10. Вычислить 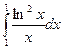 .
.
Р е ш е н и е. Положим lnx = t; 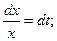 если х = l, то t =0, если х =l, то t =1.
если х = l, то t =0, если х =l, то t =1.
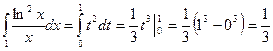
Пример 11. Вычислить 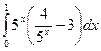
Р е ш е н и е. Выполним действия под знаком интеграла и применим табличные интегралы (1). При этом получим:
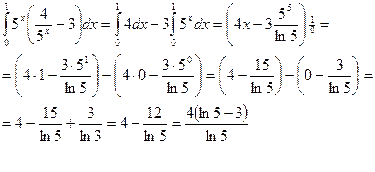
§3. Приложение определенного интеграла.
Интегральное исчисление даёт общий приём вычисления площадей плоских фигур, объемом тел вращения, работы, силы и др. Этот приём необходимо изучить по учебнику.
Пример 1. Вычислить площадь фигуры, ограниченной линиями
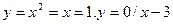
Р е ш е н и е. Сделаем чертеж (рис.1) находим
S= 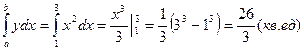
 Пример 2. Вычислить площади фигур, ограниченной линиями
Пример 2. Вычислить площади фигур, ограниченной линиями 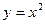 и
и 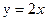 . у
. у


 у-х2
у-х2
 9 у
9 у


 6 у-2х
6 у-2х
4



 3
3
 |  |  |
 -3 -1 1 3 х
-3 -1 1 3 х
Рис. 1 Рис. 2
Р е ш е н и е. Сделаем чертеж (рис. 2). Для нахождения пределов интегрирования решим систему уравнений относительно х:
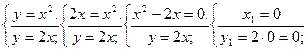 или
или 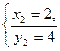
Далее имеем:
S 1= 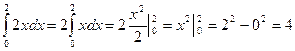 (кв. ед.)
(кв. ед.)
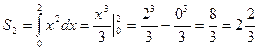 (кв. ед.)
(кв. ед.)
S = S 1- S 2=4-2 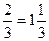 (кв.ед.)
(кв.ед.)
Пример 3. Вычислить площадь фигуры, ограниченной линиями y =cos x,
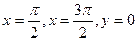
 y
y
 y
y



1 y =cos x
 -π/2 π/2 π 3π/2 x -1 0 ½ 1 2 x
-π/2 π/2 π 3π/2 x -1 0 ½ 1 2 x
Рис.3
-2¼
Рис. 4
Решение. Сделаем чертёж (рисунок 3). Имеем:
S= 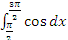 =-sin 3π/2+sinπ/2=1-(-1)=2 (кв.ед.)
=-sin 3π/2+sinπ/2=1-(-1)=2 (кв.ед.)
 2015-04-01
2015-04-01 4648
4648








