Методом Р. Беллмана

В соответствии с постановкой задачи о замене оборудования, приведенной в разд. 4.1, для функции (4.2.3) можно записать:

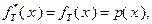(4.3.1)

где 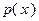– годовая прибыль, получаемая от использования оборудования возраста 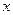. Если возраст оборудования меньше максимально допустимого значения (т.е. 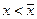), то, в соответствии с (4.2.4), запишем:

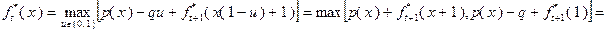
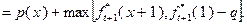(4.3.2)

Условно оптимальным управлением 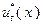здесь является то из значени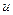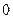й ( или 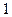), на котором достигается максимум (4.3.2). Поэтому выбор того или иного управления в качестве условно оптимального определяется следующими условиями:

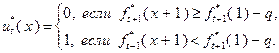(4.3.3)

Если возраст оборудования в 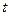-м календарном году равен максимально допустимому (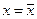), то в конце этого года однозначно происходит замена оборудования и в этом случае вместо (4.3.2) можно записать:

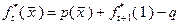, (4.3.4)

что соответствует .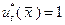

Если возраст оборудования в начальном состоянии 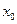не задан и существует возможность выбора оборудования разного возраста, то значение 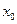может быть определено в результате решения оптимизационной задачи 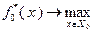. Используя 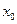и найденные условно оптимальные управления, можно получить траекторию рассматриваемой системы.

Пример 4.3.1

Рассмотрим задачу о замене оборудования (4.1.3) со следующими исходными данными: .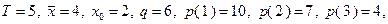

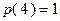В процессе решения задачи будем заполнять две таблицы: табл. 4.3.1 и табл. 4.3.2. В первую будем вносить значения функций Беллмана, во вторую – значения условно оптимальных управлений.

В соответствии с (4.3.1), последнюю строку табл. 4.3.1 заполняем значениями 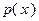, взятыми из исходных данных. Вычисление последующих значений функций 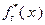, 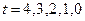при значениях аргумента 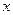, равных 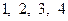, производится в соответствии с соотношениями (4.3.2) и (4.3.4), которые можно представить в следующем объединенном виде:

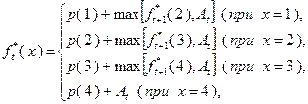(4.3.5)

где .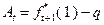

Параллельно с заполнением табл. 4.3.1 значениями функций, вычисленными с использованием выражения (4.3.5), в табл. 4.3.2 вносятся значения условно оптимальных управлений, найденных в соответствии с (4.3.3) или, что то же самое применительно к рассматриваемому примеру, с помощью следующих условий, в которых величина 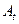имеет тот же смысл, что и в (4.3.5):

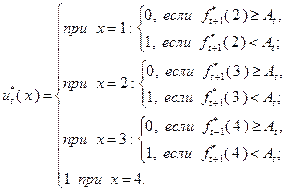
Ниже приведены расчеты значений, представленных в таблицах 4.3.1 и 4.3.2.

При : ;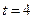

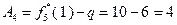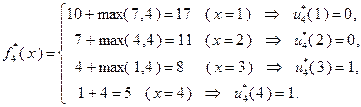
При : ;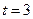

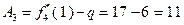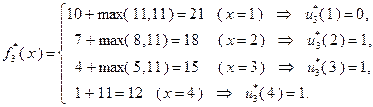
При : ;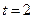

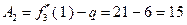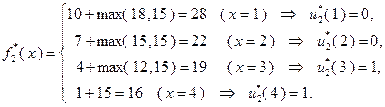
При : ;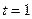

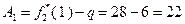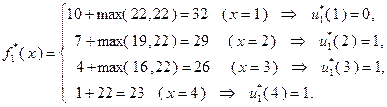
При : ;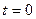

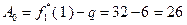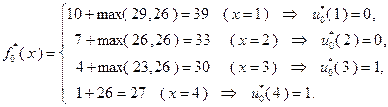
Таблица 4.3.1 Таблица 4.3.2

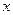
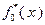
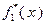
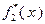
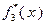
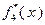
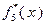
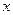
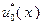
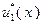
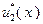
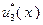
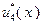
Согласно исходным данным, 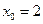, поэтому 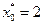. В соответствии с результатами, представленными в табл. 4.3.2, 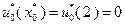. Поэтому в конце первого года работы замена оборудования не производится. В течение второго года работы возраст оборудования равен 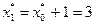, и поскольку 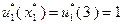, в конце второго года осуществляется замена оборудования. Следовательно, в течение третьего года возраст оборудования равен 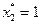, и так как 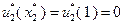, в конце третьего года замена оборудования не производится. В течение четвертого года возраст оборудования составляет 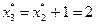, причем 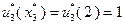, что означает замену оборудования в конце четвертого года. В течение пятого года возраст оборудования равен 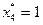и поскольку 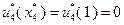, в конце пятого года замена оборудования не производится. Следовательно, в течение шестого года работы возраст оборудования составит .

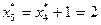В соответствии с полученными результатами, оптимальной стратегией является замена оборудования после второго и четвертого года.