1) Задача использования сырья
Для изготовления двух видов продукции 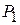 и
и 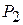 используют 3 вида сырья
используют 3 вида сырья 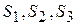 . Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемой от реализации продукции, приведены в таблице 3.1.
. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемой от реализации продукции, приведены в таблице 3.1.
Необходимо составить такой план выпуска продукции, чтобы при её реализации получить максимальную прибыль.
Таблица 3.1. Таблица показателей для задачи использования сырья
| Вид сырья | Запас сырья | Количество единиц сырья, идущих на изготовление единицы продукции | |
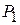
| 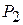
| ||
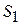
| |||
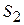
| |||
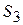
| |||
| Прибыль от единицы продукции, руб. |
Пусть 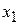 - количество единиц продукции
- количество единиц продукции 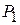 ,
, 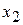 - количество единиц продукции
- количество единиц продукции 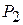 . Тогда учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:
. Тогда учитывая количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также запасы сырья, получим систему ограничений:
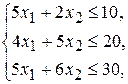 (3.1)
(3.1)
которая показывает, что количество сырья, расходуемого на изготовление продукции, не может быть больше имеющихся запасов.
Если 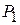 не выпускается, то
не выпускается, то 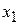 =0, в противном случае
=0, в противном случае 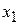 >0. Аналогично, если
>0. Аналогично, если 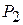 не выпускается, то
не выпускается, то 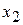 =0, в противном случае
=0, в противном случае 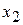 >0, т.е.
>0, т.е.
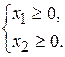 (3.2)
(3.2)
Реализация 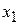 единиц продукции
единиц продукции 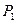 и
и 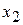 единиц продукции
единиц продукции 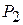 дает соответственно 30
дает соответственно 30 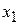 и 45
и 45 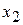 руб. прибыли. Суммарная прибыль:
руб. прибыли. Суммарная прибыль:
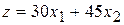 .
.
Необходимо найти такие 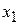 и
и 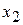 , при которых функция z достигает максимума.
, при которых функция z достигает максимума.
z называется целевой функцией и вместе с системой ограничений (3.1) и (3.2) образует математическую модель экономической задачи.
Задачу можно легко обобщить (таблица 3.2).
Таблица 3.2. Таблица показателей для задачи использования сырья
| Вид сырья | Запасы сырья | Количество единиц i-го сырья, идущего на изготовление единицы j-ой продукции | ||||
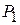
| 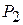
| 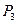
| … | 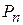
| ||
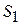
| 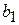
| 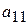
| 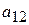
| 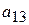
| … | 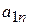
|
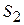
| 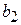
| 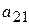
| 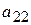
| 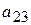
| … | 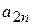
|
| … | … | … | … | … | … | … |
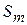
| 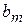
| 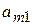
| 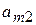
| 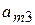
| … | 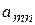
|
| Прибыль | 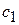
| 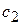
| 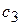
| … | 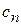
|
Пусть при выпуске n видов продукции используется m видов сырья. Обозначим через 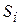 виды сырья (i= 1,2,…, m);
виды сырья (i= 1,2,…, m); 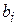 - запасы сырья i -го вида;
- запасы сырья i -го вида; 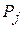 - виды продукции (j= 1,2,…, n);
- виды продукции (j= 1,2,…, n); 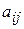 - количество единиц i- го сырья, идущего на изготовление единицы j- ой продукции;
- количество единиц i- го сырья, идущего на изготовление единицы j- ой продукции; 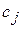 - величину прибыли, получаемой при реализации единицы j- ой продукции.
- величину прибыли, получаемой при реализации единицы j- ой продукции.
Пусть 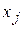 - количество единиц j- ой продукции, которое необходимо произвести.
- количество единиц j- ой продукции, которое необходимо произвести.
Целевая функция 
 .
.
Система ограничений:
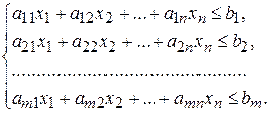
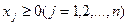 ,
,
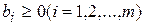 .
.
2) Задача составления рациона
При откорме каждое животное должно ежедневно получить не менее 8 единиц питательного вещества 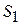 , не менее 6 единиц вещества
, не менее 6 единиц вещества 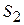 и не менее 10 единиц вещества
и не менее 10 единиц вещества 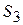 . Для составления рациона используют 2 вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице:
. Для составления рациона используют 2 вида корма. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в таблице:
Таблица 3.3. Таблица показателей для задачи составления рациона
| Питательные вещества | Количество единиц питательных веществ в 1 кг корма | |
| Корм 1 | Корм 2 | |
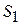
| ||
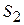
| ||
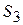
| ||
| Стоимость 1 кг корма, руб. |
Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.
Пусть 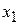 - количество килограмм корма 1,
- количество килограмм корма 1, 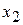 - количество килограмм корма 2 в дневном рационе.
- количество килограмм корма 2 в дневном рационе.
Т.к. дневной рацион удовлетворяет требуемой питательности только в том случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений:
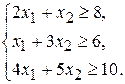 (3.3)
(3.3)
Если корм 1 не используется, то 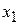 =0, в противном случае
=0, в противном случае 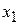 >0. Аналогично, если корм 2 не выпускается, то
>0. Аналогично, если корм 2 не выпускается, то 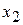 =0, в противном случае
=0, в противном случае 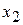 >0, т.е.
>0, т.е.
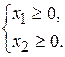 (3.4)
(3.4)
Необходимо добиться минимальных затрат на дневной рацион, т.е.
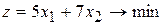 .
.
Задачу можно обобщить, если предусмотреть в рационе m видов питательных веществ в количестве не менее 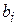 (i= 1,2,…, m) единиц и использовать n видов кормов.
(i= 1,2,…, m) единиц и использовать n видов кормов.
Для составления математической модели задачи обозначим 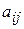 (j= 1,2,…, n) - количество единиц i- го питательного вещества, содержащегося в единице j- го корма;
(j= 1,2,…, n) - количество единиц i- го питательного вещества, содержащегося в единице j- го корма; 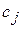 - стоимость единицы j- го корма.
- стоимость единицы j- го корма.
Пусть 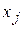 - количество единиц j- го корма в дневном рационе.
- количество единиц j- го корма в дневном рационе.
Необходимо найти минимальное значение линейной функции

при ограничениях
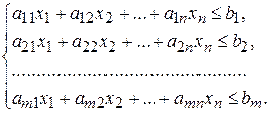
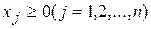 ,
, 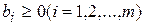 .
.
 2015-04-01
2015-04-01 650
650








