Вектор полных затрат

Для получения валового выпуска 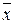, обеспечивающего конечное потребление 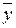, нужно прежде всего произвести набор товаров, описываемый вектором 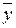. Но этого мало - ведь для получения 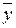нужно затратить продукцию, описываемую вектором А 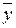. Но и этого мало - для получения А 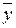нужно осуществить дополнительные затраты, описываемые вектором А (А 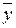)= А ² 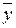, и т.д. 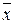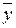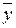В итоге приходим к заключению, что весь валовой выпуск должен составляться из слагаемых , А , А ² 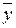. В соответствии с этим рассуждением сумму 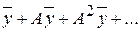называют вектором полных затрат, а сделанное выше заключение формулируют так: вектор валового выпуска 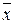совпадает с вектором полных затрат.

Чтобы сделать это заключение более конкретным, рассмотрим такой пример. Пусть речь идет о блоке из трех промышленных отраслей: металлургия, электроэнергетика, угледобыча.

Для получения конечного выпуска 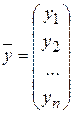необходимо, прежде всего, произвести 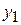т металла; 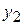кВт. ч. электроэнергии; 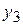т угля.

Но для производства 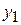т металла, в свою очередь, необходимо затратить (а значит, сначала произвести) какие-то количества металла 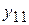, электроэнергии 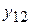и угля 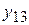. Точно также для производства 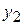кВт. ч. электроэнергии необходимо затратить 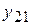металла, 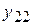электроэнергии и 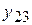угля, аналогично для производства 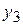т угля нужно затратить 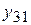металла, 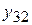электроэнергии и 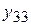угля.

В свою очередь, для производства 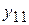т металла необходимо затратить какие-то количества металла, электричества и угля и т.д. Искомый валовой выпуск 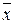представляет собой сумму затрат нулевого порядка (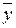), первого порядка (А 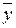), второго порядка (А ² 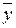) и т.д.

Пример 2.5. Для трех отраслей задана межотраслевые потоки (таблица 2.2) и конечный продукт (таблица 2.3).

Таблица 2.2. Межотраслевые потоки Таблица 2.3. Конечный продукт

Отрасли	1	2	3						Отрасли	Конечный продукт
1	45,65	3,52	17,25						1	61,56
2	4,58	35,86	0,86						2	84,24
3	14,56	0,58	16,49						3	46,12

Постройте межотраслевой баланс в отчетном периоде и, увеличив конечный продукт на 10 %, постройте межотраслевой баланс в плановом периоде в стоимостном выражении в соответствии с таблицей 2.4.

Таблица 2.4. Межотраслевой баланс

Отрасли	1	2	3	Итого	Конечный продукт	Валовой продукт
1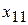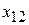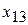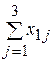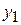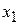
2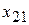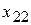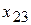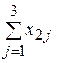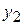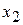
3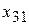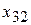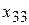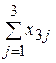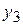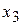
Итого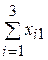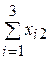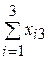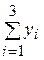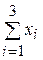
Чистая продукция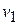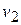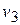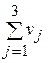
Всего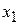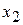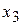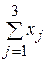

Решение.

1. Построим межотраслевой баланс в отчетном периоде и занесем в таблицу 2.5:

Таблица 2.5. Межотраслевой баланс в отчетном периоде

Отрасли	1	2	3	Итого	Конечный продукт	Валовой продукт
1	45,65	3,52	17,25	66,42	61,56	127,98
2	4,58	35,86	0,86	41,3	84,24	125,54
3	14,56	0,58	16,49	31,63	46,12	77,75
Итого	64,79	39,96	34,6	139,35	191,92	331,27
Чистая продукция	63,19	85,58	43,15	191,92
Всего	127,98	125,54	77,75	331,27

2. Построим межотраслевой баланс в плановом периоде.

Найдем матрицу А прямых затрат, элементы которой рассчитаем по формуле

.

.

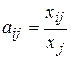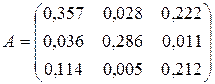Она имеет неотрицательные значения и удовлетворяет критерию продуктивности:

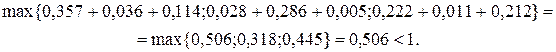
Поэтому для любого вектора конечного продукта 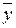можно найти необходимый объем валового выпуска по формуле:

Матрица

.

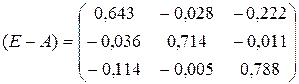Обратная к ней матрица имеет вид:

.

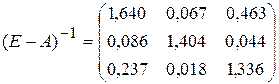Посчитаем величину конечного продукта в плановом периоде, увеличив на 10 %

.

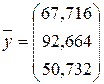Определим величину валовой продукции в плановом периоде:

= .

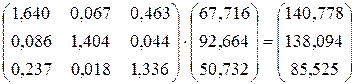Посчитаем межотраслевые потоки в плановом периоде по формуле 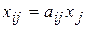и построим баланс в плановом периоде (таблица 2.6).

Таблица 2.6. Межотраслевой баланс в плановом периоде

Отрасли	1	2	3	Итого	Конечный продукт	Валовой продукт
1	50,215	3,872	18,975	73,062	67,716	140,778
2	5,038	39,446	0,946	45,43	92,664	138,094
3	16,016	0,638	18,139	34,793	50,732	85,525
Итого	71,269	43,956	38,06	153,285	211,112	364,397
Чистая продукция	69,509	94,138	47,465	211,112
Всего	140,778	138,094	85,525	364,397