Задана математическая модель:
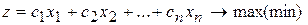 , (3.19)
, (3.19)
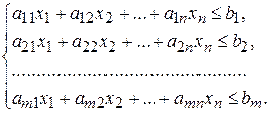 (3.20)
(3.20)
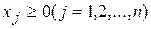 ,
, 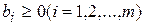 . (3.21)
. (3.21)
Каждое из неравенств системы ограничений (3.20) и (3.21) является полупространством с граничными гиперплоскостями
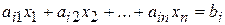 , (
, (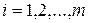 ),
),
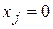 , (
, (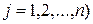 .
.
Пересечение полупространств, заданных системой ограничений, если она совместна, будет выпуклым многогранником, который образует область допустимых решений (ОДР) системы ограничений.
Любая внутренняя и граничная точка ОДР является решением задачи. Приравняем функцию (3.19) к нулю, тогда уравнение
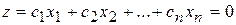
представляет собой гиперплоскость, проходящую через начало координат и перпендикулярную вектору-градиенту. Направление вектора-градиента показывает направление возрастания функции. Поэтому, чтобы найти максимум функции, нужно передвигать гиперплоскость в направлении вектора как можно дальше от начала координат, но чтобы она имела с ОДР хотя бы одну общую точку. Чтобы найти минимум функции, нужно определить ближайшую точку в ОДР от начала координат.
Для двумерного пространства на рис. 3.1 показано, что в угловой точке А максимальное значение функции, а в точке В - минимальное.
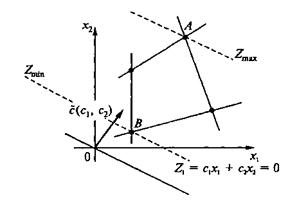
Рис.3.1. Область допустимых решений задачи с максимальным и минимальным значениями в угловых точках
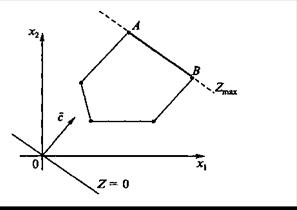
Рис. 3.2. Область допустимых решений задачи с множеством решений
Рис. 3.2 отражает случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции 2 достигается в точке А и в точке В, следовательно, и в любой точке отрезка АВ, так как эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
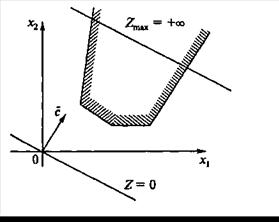
Рис. 3.3. Множество, неограниченное сверху
На рис. 3.3 изображен вариант, когда система ограничений образует неограниченное сверху множество. Функция z при этом стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко.
На рис. 3.4 представлен случай несовместной системы ограничений.
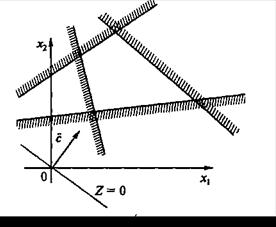
Рис. 3.4. Несовместная система ограничений
 2015-04-01
2015-04-01 516
516








