Продуктивные модели Леонтьева

Определение. Матрица А 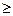0 называется продуктивной, если для любого вектора 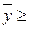0 существует решение 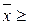0 уравнения

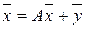. (2.7)

В данном случае и модель Леонтьева, определяемая матрицей А, тоже называется продуктивной. Другими словами, модель продуктивна, если любое конечное потребление 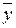можно обеспечить при подходящем валовом выпуске .

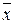Уравнение Леонтьева (2.7) можно записать следующим образом:

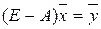, (2.8)

где Е - единичная матрица. Возникает, естественно, вопрос об обращении матрицы 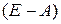. Понятно, что если обратная матрица 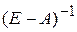существует, то из (2.8) вытекает

. (2.9)

Теорема 2.3 (первый критерий продуктивности). Матрица А 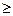0 продуктивна тогда и только тогда, когда матрица 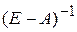существует и неотрицательна.

Пример 2.3. Исследовать на продуктивность матрицу

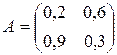
Решение. В данном случае

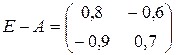
Необходимые вычисления предоставим читателю провести самостоятельно. Получаем матрицу

,

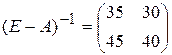все элементы которой неотрицательны. Следовательно, А продуктивна.