Решение. Решение сформулированной задачи найдем, используя геометрическую интерпретацию

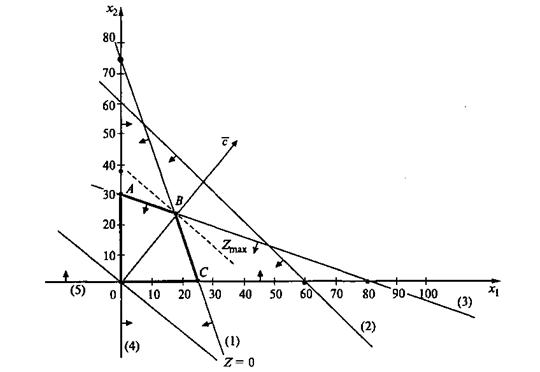
Решение сформулированной задачи найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений-неравенств запишем в виде уравнений и пронумеруем их:

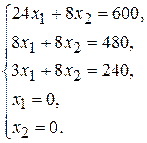
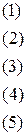
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.

Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: при 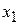=0, 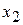=75, а при 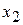=0, 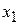=25. Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем любую точку на плоскости, не лежащую на прямой, например, точку 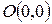и подставим ее координаты в неравенство - оно является верным. Так как точка О (0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой 24 +8 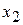=600. На рисунке расположение полуплоскости относительно первой прямой отмечено стрелками.

Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенствам. Точки, удовлетворяющие ограничениям 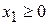, , 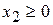находятся в первом квадранте.

Множество точек, удовлетворяющих всем ограничениям одновременно, является областью допустимых решений системы ограничений. На графике это многоугольник ОАВС.