Метод невзвешенного попарного среднего

В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние (сходство) между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные "рощи", однако он работает одинаково хорошо и в случаях протяженных ("цепочного" типа) кластеров. В литературе [3] используют сокращение UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего - unweighted pair-group method using arithmetic averages. Для документной кластеризации этот метод дает наилучшие результаты. Вычисление близости может идти по следующей формуле, использующей меру сходства косинуса [3]:

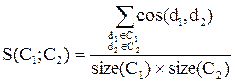, (37)

где С₁,С₂ – кластеры, size(C₁),size(C₂) – размер кластеров (количество документов), d₁,d₂ – документы, принадлежащие соответствующим кластерам.

Вообще, идея метода попарного среднего состоит в предположении, что объекты входящие в подкластеры, принадлежащие одному кластеру близки друг другу. Таким образом, объединяя кластеры с наиболее близкими объектами можно получить кластер, плотность (значение выбранной меры внутреннего сходства или связности) которого максимальна на данном этапе объединения.

Такой подход может находить кластеры разной формы и размеров, однако, объединение кластеров разной формы на поздних этапах объединения для него подчас становиться проблематичным. Существует схожий метод, предполагающий, что не всегда стоит брать в расчет сходства между всеми парами объектов.

Этот подход вводит понятия взаимной связности и связи, а также предположение о том, что кластер размера n имеет n^q связей, где .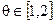

Связь – это величина, характеризующая отношение между двумя объектами, возникающее тогда, когда значение близости между этими двумя объектами превышает заданный порог. В графоориентированной кластеризации связь считают ребром.

Если для установления связи используются любые значения близости (пороговое значение равно 0), то число связей каждого объекта в кластере равно размеру этого кластера. Взаимная связность между двумя кластерами – это общее число связей между объектами двух кластеров, принадлежащих разным кластерам.

Предположим, есть два кластера A и B, размера n и m, соответственно. Если A и B принадлежат какому-то одному кластеру, то в нем будет 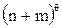связей. При этом, n^q и m^q связей будут принадлежать кластерам A и B, а 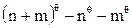связей будут между объектами кластеров A и B. Таким образом, сходство между кластерами A и B может быть подсчитано, как [42]:

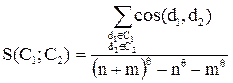. (38)

В числителе подсчитываются только веса (или число) связей, определяемых значением q.

Особенностью данного подхода является использование модели взаимной связности, определяемой пользователем с помощью параметра q. Так, данный метод, практически, идентичен предыдущему (UPGMA), если q = 2.

Похожий подход с использованием заданной заранее моделью связности применяется в алгоритме ROCK в [38] и ему подобных. В этих методах рассматриваются не все связи, а только превышающие заданный порог.

Временная сложность алгоритмов кластерного анализа, использующих метод объединения по принципу взвешенного попарного среднего обычно выражается как O(N²). Пространственная сложность выражается как O(N).