Транспортная задача является частным случаем ЗЛП или частным случаем задачи оптимизации сетей, применяется при решении плановых задач выбора маршрутов перевозок. В общем виде формулируется следующим образом. Пусть рассмотрено m различных поставщиков (пунктов отправления) Pi, располагающих некоторой однородной продукций соответственно в количествах ai 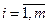 , и рассматривается отправление этой продукции в n пунктов потребления Qj, j=
, и рассматривается отправление этой продукции в n пунктов потребления Qj, j= 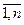 , потребности которых равны bj cоответственно. Известны тарифы перевозок этой продукции из пункта Pi в пункт Qj (затраты на перевозку единицы груза) Cij. Требуется составить такой план перевозок, чтобы общая стоимость затрат была минимальной.
, потребности которых равны bj cоответственно. Известны тарифы перевозок этой продукции из пункта Pi в пункт Qj (затраты на перевозку единицы груза) Cij. Требуется составить такой план перевозок, чтобы общая стоимость затрат была минимальной.
К этой задаче возможно дополнение об ограничениях по пропускным способностям, о существовании промежуточных пунктов перезагрузки, источников и стоков груза. Математическая модель этой задачи имеет вид:
Xij – количество едениц груза из i в j пункт.
ƒ= 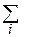
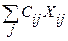 →min
→min
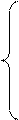
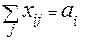
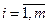
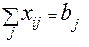 j=
j= 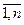
xij≥0.
Учитывая, что эта задача является частным случаем ЗЛП, рассматриваются специальные способы решения этих задач.
Транспортная таблица задачи имеет вид:
| Qj Pi | Q1 | Q2 | … | Qn | Запасы |
| P1 | X11 c11 | X12 c12 | … | X1n c1n | a1 |
| P2 | X21 c21 | X22 c22 | … | X2n c2n | a2 |
| … | … | … | … | … | … |
| Pm | Xm1 cm1 | Xm2 cm2 | … | Xmn cmn | am |
| Потребность | b1 | b2 | … | bn |
Транспортная задача имеет решение, если ∑ai=∑bj (закрытая модель).
Если ∑ai < ∑bj, то вводят фиктивный пункт производства, и не все пункты в оптимальном решении будут удовлетворены в потребности.
Если ∑ai>∑bj, то не все запасы будут вывезены из пунктов производства, в решении вводят фиктивный пункт потребления. Заметим, что объем продукции в фиктивном пункте равен разности │∑ai -∑bj│.
Циклом в транспортной таблице называют замкнутую ломаную линию, удовлетворяющую следующим условиям:
1. Все вершины ломаной находятся в клетках транспортной таблицы.
2. Ребра расположены по строкам или столбцам, но не диагоналям.
3. К каждой вершине подходят 2 ребра: одно - по строке, другое - по столбцу транспортной таблицы.
4. Набор клеток транспортной таблицы называется ацикличным, если не существует цикла, все вершины которого находятся в клетках этого набора.
Теорема. Допустимое решение транспортной задачи является опорным, т.и.т.т.к. набор заполненных клеток ацикличен, т.е. в него входит m+n-1 клетка.
Определение. Потенциалом опорного решения α транспортной задачи называют числа Ui 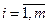 , Vj j=
, Vj j= 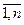 , такие что Ui+Vj=Cij – тариф заполненной клетки.
, такие что Ui+Vj=Cij – тариф заполненной клетки.
Теорема ( Достаточное условие оптимальности опорного решения). Если для всех незаполненных клеток (i,j) Ui+Vj=Cij, где Ui и Vj - потенциалы опорного решения α, тогда это опорное решение является оптимальным.
Методы построения опорных решений:
1. Метод северо-западного угла. Начинаем заполнение с клетки (1,1) – северо-западного угла таблицы либо удовлетворяя потребность, либо исчерпывая запасы в этом пункте. Затем переходим в следующий столбец или строку, что зависит от наличия потребности и запасов, идя как бы по диагонали таблицы, заканчиваем заполнение в клетке (m,n), получая опорное решение.
2. Метод минимального элемента. Среди всех клеток выбираем клетку с наименьшим тарифом Cks и начинаем заполнение с этой клетки либо удовлетворяя потребность, либо исчерпывая запасы (если таких клеток несколько, то заполняем все эти клетки). Затем переходим к заполнению клеток с большими по величине тарифами, пока полностью не исчерпаем запасы или не удовлетворим потребности.
Метод аппроксимации Фогеля. На любой итерации находим по всем строкам и всем столбцам разность между двумя минимальными тарифами и записываем их в специальной строке и столбце таблицы. Среди разностей выбираем минимальную. В строке или столбце, соответствующим этой разности, находим минимальный тариф и клетку с этим тарифом заполняем на данной итерации либо исчерпывая запасы, либо удовлетворяя потребности. Если минимальный тариф одинаков для нескольких клеток выбранной строки или столбца, то для заполнения выбираем ту клетку, которая расположена в столбце или строке соответственно с наибольшей разностью между двумя минимальными тарифами этого столбца или строки.
Замечание: Если заполненных клеток оказалось меньше чем m+n-1, то к полученному набору дописывают в некоторых клетках «0», так чтобы общее количество заполненных клеток стало m+n-1.
Алгоритм решения транспортной задачи методом потенциалов.
1. Построить опорное решение транспортной задачи тремя описанными выше методами. Для каждого опорного решения найти значение целевой функции и остановится на том, для которого это значение минимально.
2. Найти потенциалы заполненных клеток.
3. Для незаполненных клеток проверить условие оптимальности. Если условие оптимальности выполняется, то полученное решение оптимально.
4. В противном случае выбирают клетку (k,s), для которой Uk+Vs>Cks и строим цикл транспортной таблицы, приписывая клетке знак «+» и чередуя знаки во всех остальных клетках цикла.
5. Проводим пересчет таблицы по следующему правилу. Необходимо выбрать число r=min xij из клеток цикла, помеченных знаком «-». В клетках цикла, помеченных знаком «+», это число прибавляем. В клетках цикла, помеченных знаком «-», это число отнимаем. Остальные клетки цикла не изменяем, и ту клетку, в которой было найдено r, не заполняем.
6. Возвращаемся к пункту 2.
Пример. Решить транспортную задачу
| B1 | B2 | B3 | B4 | Потребности | |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| Запасы |
Составим опорное решение методом северо-западного угла:
| B1 | B2 | B3 | B4 | Потребности | |
| A1 | 270 1 | 140 4 | 100 7 | ||
| A2 | 90 8 | ||||
| A3 | 10 4 | 110 8 | |||
| Запасы |
ƒ(α1)=270+560+700+720+40+880=3170
 2015-04-01
2015-04-01 1576
1576
