Условие оптимальности выполняется, поэтому получено оптимальное решение

ƒ(α_опт)=270+520+330+720+20+440=2300

α_опт=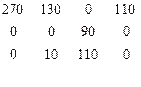

6 Задача о назначениях

Задача о назначениях является частным случаем транспортной задачи. Известно, что каждую из m работ могут выполнять любые из n исполнителей. Стоимость выполнения j работы i исполнителем равна C_ij. Нужно распределить исполнителей по рабочим местам так, чтобы минимизировать затраты или если C_ij – эффективность работы j исполнителя на i месте, нужно распределить исполнителей с целью оптимизации эффективности.

Математическая модель задачи, если сводить ее к транспортной задаче, примет вид:

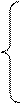
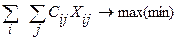
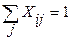
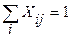
X_ij≥0

Однако улучшенным алгоритмом решения этой задачи является венгерский алгоритм:

1. Редукция строк и столбцов:

- в строке выбирается наименьший элемент, который вычитается из всех элементов строки;

- в столбце выбирается наименьший элемент, который вычитается из элементов этого столбца.

2. Если некоторое решение в матрице является допустимым, то есть в каждой строке и каждом столбце находится только один нулевой элемент, то проводится назначение: если a_ij = 0, то i-ый работник выполняет j-ую работу.

Если же допустимых решений нет, то:

2.1. Находится строка, содержащая только одно нулевое значение. В клетке, соответствующей нулевому значению, делается назначение. Если такие строки отсутствуют, выбирается любое нулевое значение.

2.2. Зачеркиваются оставшиеся нулевые значения данного столбца

2.3. Пункты 1 и 2 повторять до тех пор, пока это возможно.

Если на данном этапе окажется, что есть несколько нулей, которым не соответствуют назначения и которые не зачеркнуты, то необходимо:

2.4. Найти столбец, содержащий только один ноль, делается назначение в этой клетке.

2.5. Зачеркиваются остальные нули в данной строке.

2.6. Повторять пункты 4 и 5 до тех пор, пока это возможно.

Если решение является допустимым, т.е. все элементы распределены в клетки, которым соответствует нулевая стоимость, то полученное решение является оптимальным. Если окажется, что матрица содержит неучтенные нули, то полученное решение является недопустимым и происходит переход к шагу 3

3. Модификация матрицы. Проводится минимальное число прямых через строки и столбцы так, чтобы они проходили через все нули в матрице. Находится наименьший из элементов, через которые не проходит ни одна из проведенных прямых. Вычитается этот элемент из всех элементов, через которые не проходит ни одна из проведенных прямых. Прибавляется этот элемент ко всем элементам, лежащим на пересечении проведенных ранее прямых. Остальные элементы не изменяются. В результате этого шага появляются новые нулевые элементы. Далее возвращаются ко 2-му шагу и повторяют алгоритм до получения допустимого решения.

Пример. Разместить датчики на 4 объектах так, чтобы стоимость размещения была минимальна. Известна матрица стоимости назначений

С =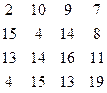

Решение.

1.Редукция матрицы:

min

С = → →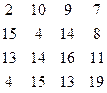

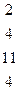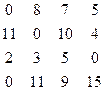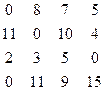
min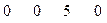

2. Назначение 0 8 7 5 получилось недопустимым.

11 0 10 4

2 3 5 0

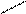0 11 9 15

3. Модификация.

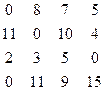
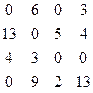
2. Повторяем назначение: 0 6 0 3. Это назначение допустимо,

13 0 5 4 поэтому решение получено.

4 3 0 0

0 9 2 13

Общая стоимость назначения = (9+4+11+4)=28

Замечание. При решении задачи максимизации (при поиске наиболее эффективного назначения) нужно целевую функцию умножить на -1, а затем применить венгерский алгоритм. Полученное допустимое решение перенести в первоначальную матрицу.