Решение задач линейного программирования двойственным симплекс-методом

Если среди свободных членов системы ограничений есть отрицательный, то используется двойственный симплекс-метод.

Определение. Псевдопланом ЗЛП в канонической форме называют такой вектор 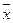(b₁, b₂, … b_n, 0,…,0), все оценки которого в некотором базисе положительны для задачи максимизации, а среди координат есть отрицательные.

Свойства псевдоплана.

1. Если в ЗЛП существует b_i <0, а все элементы i-ой строки симплекс-таблице положительны, то задача не имеет решения.

2. Если в ЗЛП b_i<0 и в i – ой строке симплекс таблицы есть отрицательные элементы, то можно перейти к новому псевдоплану, при котором значение целевой функции задачи максимизации не уменьшится.

Алгоритм двойственного симплекс-метода для задачи максимизации.

1. Найти псевдоплан задачи.

2. Проверить псевдоплан на оптимальность. Если условие оптимальности выполняется, т.е. все оценки неотрицательны, и все компоненты вектора 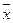также неотрицательны, то 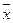- оптимальное решение получено.

3. Если условие неразрешимости выполняется, то решения задачи не существует.

4. Если условие неразрешимости не выполняется, то переходят к новому псевдоплану. Выбирают направляющую строку, определив наибольшее по абсолютной величине отрицательное число столбца вектора 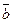, и направляющий столбец, определив минимальное по абсолютной величине отношение положительных элементов строки оценок к соответствующим отрицательным элементам направляющей строки.

5. Производят пересчет таблицы по правилу жордановых преобразований.

6. Возвращаемся к пункту 2.

Пример. Ежедневно животные, выращиваемые на ферме, должны получать вещества A,B,C. В продуктах 1, 2, 3 эти вещества содержатся в количестве, указанном в таблице:

Продукты вещества				Минимально допустимая ежедневная норма потребления питательных веществ
A
B
C
Цена единицы продукта

Составить дневной рацион, обеспечивающий получение достаточного количества питательных веществ при минимальных затратах.

Решение. Составим математическую модель задачи. Пусть x₁,x₂,x₃ –количество продуктов вида 1,2,3 потребляемых ежедневно, тогда ограничения по количеству получаемых ежедневно питательных веществ примут вид:

x₁+3x₂+4x₃≥60 для вещества А;

2x₁+4x₂+2x₃≥50 для вещества В;

x₁+4x₂+3x₃≥12 для вещества С;

x₁,x₂,x₃ ≥0;

целевая функция означает затраты на приобретение продуктов вида 1,2,3 в количествах x₁,x₂,x₃, эти затраты составят ƒ(x₁,x₂,x₃)=9x₁+12x₂+10x₃→ min

Умножаем уравнения ограничений и целевой функции на (-1) и приводим систему ограничений к каноническому виду, прибавляя в левых частях ограничений вспомогательные переменные x₄,x₅,x₆:

-x₁-3x₂-4x₃+x₄=-60

-2x₁-4x₂-2x₃+x₅=-50

-x₁-4x₂-3x₃+x₆=-12

G(x₁,x₂,x₃)=-ƒ(x₁,x₂,x₃)=-9x₁-12x₂-10x₃→ max

Базис	B	X1	X2	X3	X4	X5	X6
X4	-60	-1	-3	-4
X5	-50	-2	-4	-2
X6	-12	-1	-4	-3
Оценки
Базис	B	X1	X2	X3	X4	X5	X6
X3		1/4	3/4		-1/4
X5	-20	-1,5	-2,5		-0,5
X6		-1/4	-7/4		-3/4
Оценки	-150	6,5	4,5		2,5
Базис	B	X1	X2	X3	X4	X5	X6
X3		-115			-0,4	0,3
X2		0,6			0,2	-0,4
X6		4/5			-0,4	-0,7
Оценки	-186	3,8			1,6	1,8

Т.к. условие оптимальности выполняется, и псевдоплан преобразован в оптимальное решение, то выписываем из столбца 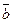искомые значения X₁=0; X₂=8; X₃=9 – необходимое количество продуктов 1,2,3 соответственно, которые позволяют организму получить питательные вещества в требуемых количествах, а переменные X₄=0; X₅=0; X₆=19 показывают превышение нормы поступления питательных веществ А, В, С.