Переходный процесс возникает в электрических цепях, при различного рода воздействиях (подключении к цепи или отключении от цепи источников электрической энергии, а также при скачкообразном изменении схемы цепи или параметров входящих в нее элементов), которые называются коммутациями. Коммутация осуществляется с помощью идеального ключа: сопротивление ключа в разомкнутом положении равно 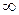 , в замкнутом – 0.
, в замкнутом – 0.

Будем считать, что коммутация происходит мгновенно 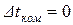 . Начало отсчёта времени t = 0 совмещается с моментом коммутации.
. Начало отсчёта времени t = 0 совмещается с моментом коммутации.
Законы коммутации:
1) Ток в индуктивности непосредственно после коммутации 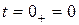 сохраняет значение, которое он имел до коммутации при
сохраняет значение, которое он имел до коммутации при 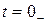 :
:
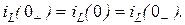
2) Напряжение на ёмкости непосредственно после коммутации 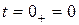 сохраняет значение, которое оно имело до коммутации при
сохраняет значение, которое оно имело до коммутации при 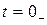 :
:
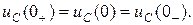
Начальные условия − значения токов и напряжений при t = 0.
Независимые начальные условия − это значения тока в индуктивности 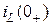 и напряжения на ёмкости
и напряжения на ёмкости 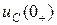 в момент коммутации t = 0, которые определяются на основании законов коммутации путем расчета установившегося режима в цепи до коммутации.
в момент коммутации t = 0, которые определяются на основании законов коммутации путем расчета установившегося режима в цепи до коммутации.
Зависимые начальные условия − это значения токов и напряжений, а также их производных в момент коммутации t = 0, которые могут изменяться скачком, например: 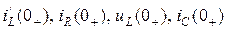 и т.п. Они определяются по схеме, образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.
и т.п. Они определяются по схеме, образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.
В данном пособии рассматриваются два метода расчета переходных процессов в линейных электрических цепях: классический и операторный.
4.1.1 Классический метод расчета.
Порядок расчета переходных процессов классическим методом:
а) определяют независимые начальные условия 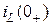 и
и 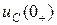 ;
;
б) записывают дифференциальные уравнения по законам Кирхгофа, искомую переменную (ток или напряжение) представляют в виде:
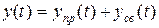 ;
;
в) определяют принуждённую составляющую 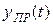 путём расчёта установившегося режима в цепи после коммутации;
путём расчёта установившегося режима в цепи после коммутации;
г) определяют свободную составляющую 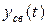 :
:
− составляют характеристическое уравнение любым методом, например, методом входного сопротивления, и вычисляют его корни;
− записывают свободную составляющую 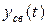 , выражение свободной составляющей
, выражение свободной составляющей 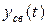 зависит от вида корней характеристического уравнения и для цепи второго порядка
зависит от вида корней характеристического уравнения и для цепи второго порядка 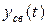 имеет вид:
имеет вид:
- при действительных и различных корнях 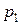 < 0 и
< 0 и 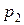 < 0
< 0
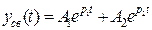 ;
;
- при действительных и равных корнях 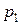 =
= 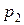 = р < 0
= р < 0
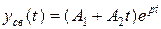 ;
;
- при комплексно-сопряжённых корнях 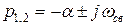 (α – коэффициент затухания, ωс в – частота свободных колебаний)
(α – коэффициент затухания, ωс в – частота свободных колебаний)
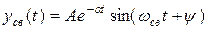
или
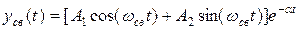 .
.
− находят постоянные интегрирования, А 1, А 2 или А, ψ. Для цепи второго порядка постоянные интегрирования определяются по начальным значениям искомой переменной и её первой производной 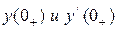 .
.
Например, если корни характеристического уравнения действительные и различные:
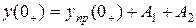 ,
, 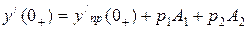 .
.
Если корни комплексно-сопряжённые:
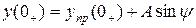 ,
, 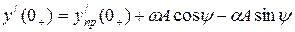 .
.
д) строят график 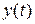 .
.
4.1.2 Операторный метод расчета.
Порядок расчета переходных процессов операторным методом:
а) определяют независимые начальные условия: 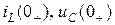 ;
;
б) составляют эквивалентную операторную схему для цепи после коммутации. Ненулевые начальные условия 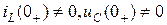 учитываются введением внутренних (расчетных) ЭДС (или источников тока): в ветвях с индуктивностью вводится ЭДС
учитываются введением внутренних (расчетных) ЭДС (или источников тока): в ветвях с индуктивностью вводится ЭДС 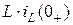 , в ветвях с емкостью вводится ЭДС
, в ветвях с емкостью вводится ЭДС 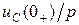 . Ниже приведены эквивалентные операторные схемы замещения пассивных элементов:
. Ниже приведены эквивалентные операторные схемы замещения пассивных элементов:
− резистивное сопротивление
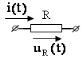
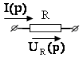
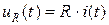 ,
, 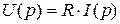 ;
;
− индуктивность

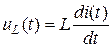 ,
, 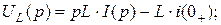
− ёмкость

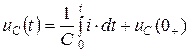 ,
, 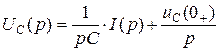 ;
;
в) рассчитывают по операторной схеме изображение искомой переменной (тока или напряжения) известными методами (законы Ома и Кирхгофа, МКТ, МУП, МЭГ и т.п.). Изображение имеет вид рациональной дроби:
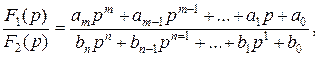
где m < n, 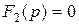 – характеристическое уравнение. Затем по изображению функции определяют ее оригинал – функцию времени;
– характеристическое уравнение. Затем по изображению функции определяют ее оригинал – функцию времени;
г) оригинал определяют по теореме разложения (см. таблицу 4.1), по таблицеоригиналов иизображений, с помощью обратного преобразования Лапласа.
Таблица 4.1 – Теорема разложения
Вид корней характеристического уравнения 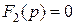 | Теорема разложения |
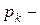 простые вещественные корни характеристического уравнения простые вещественные корни характеристического уравнения 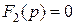 | 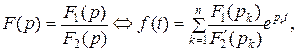 где где 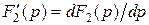 |
знаменатель имеет один нулевой корень: 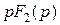 | 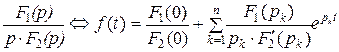 |
1. характеристическое уравнение 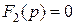 имеет простые вещественные корни имеет простые вещественные корни 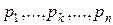 и комплексно-сопряженные корни и комплексно-сопряженные корни 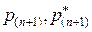 2. 2. 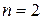 , , 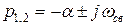 - комплексные сопряженные корни уравнения - комплексные сопряженные корни уравнения 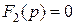 | 1. 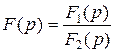 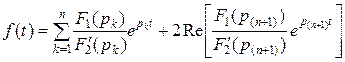 2. 2. 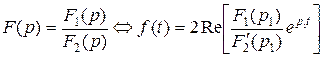 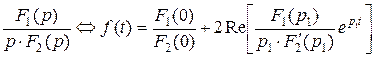 |
 2015-04-01
2015-04-01 1345
1345








