Задача 1.2.1 В электрической цепи (см. рисунок 1.1) задано:
1) 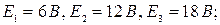
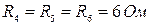 ;
;
2) показания амперметров: 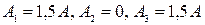 ;
;
3) мощность источников ЭДС 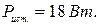
Требуется определить:
1) значения и направления токов в ветвях электрической цепи;
2) значения резисторов R 1, R 2, R 3.
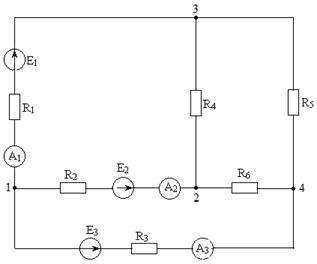
Рисунок 1.1 – Схема электрической цепи
Решение.
Определим направления токов I 1, I 3.
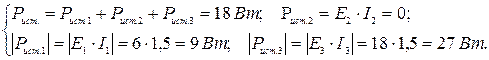
Ток I 1 должен быть направлен противоположно направлению Е 1, а ток I 3 совпадать с направлением Е 3, тогда
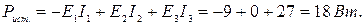
Преобразуем треугольник с одинаковыми сопротивлениями R 4= R 5 = R 6 = R = 6 Ом в эквивалентную звезду сопротивлений. Сопротивления лучей звезды
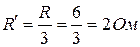 .
.
Получим эквивалентную схему, приведенную на рисунке 1.2.
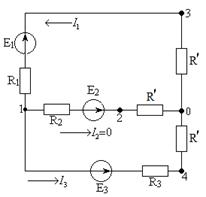
Рисунок 1.2 – Схема эквивалентной электрической цепи
Определим напряжение 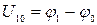 . Для простоты положим, что
. Для простоты положим, что 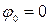 . Тогда
. Тогда 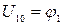 ,
, 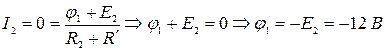 .
.
Это равенство выполняется при любом конечном значении R 2 (при 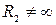 ).
).
Сопротивления R 1 и R 3 определяют из закона Ома для участка цепи:
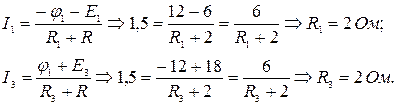
Определим потенциалы 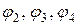 :
:
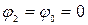 ;
;
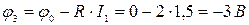 ;
;
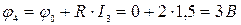 .
.
Вернемся к исходной схеме и определим токи I 4, I 5, I 6:
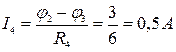 и направлен от узла 2. к. узлу 3, т.к.
и направлен от узла 2. к. узлу 3, т.к. 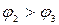 .
.
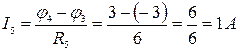 и направлен от узла 4 к узлу 3
и направлен от узла 4 к узлу 3 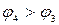 .
.
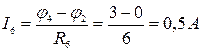 и направлен от узла 4 к узлу 2
и направлен от узла 4 к узлу 2 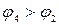 .
.
Задача 1.2.2 В электрической цепи (см. рисунок 1.3) заданы значения всех сопротивлений: 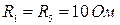 ;
; 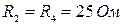 ;
; 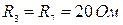 ;
; 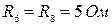 , также известно значение напряжения U ab=100 В.
, также известно значение напряжения U ab=100 В.
Требуется:
1) определить значения токов в ветвях электрической цепи;
2) проверить выполнение баланса мощностей источников и нагрузки.
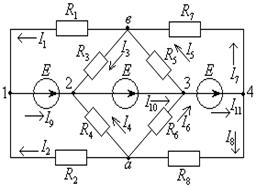
Рисунок 1.3 – Схема электрической цепи
Решение.
Примем φ 1=0, тогда 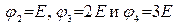 . Составим систему уравнений методом узловых потенциалов для узлов a и b:
. Составим систему уравнений методом узловых потенциалов для узлов a и b:
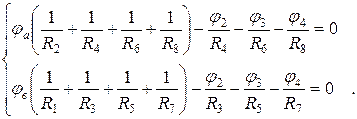 (1.1)
(1.1)
Подставим значения сопротивлений и потенциалов:
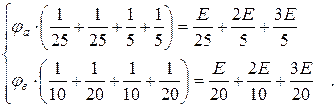 (1.2)
(1.2)
Упростим систему уравнений (1.2). Для этого умножим второе уравнение на 1,6 и вычтем его из первого, получим:
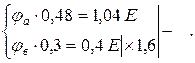 (1.3)
(1.3)
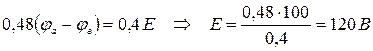 , где
, где 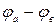 = U ab =100 В.
= U ab =100 В.
Найдем потенциалы узлов a и b, подставив в систему уравнений (1.3) найденное значение ЭДС Е =120 В:
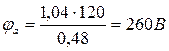 ,
, 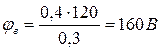 .
.
Потенциалы остальных узлов:
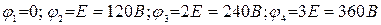 .
.
Определим токи в ветвях схемы по закону Ома для участка цепи:
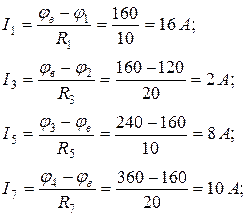
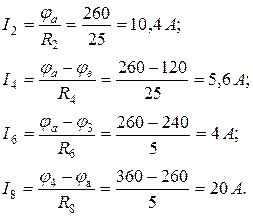
Токи в источниках ЭДС E определим из уравнений, составленных по первому закону Кирхгофа:
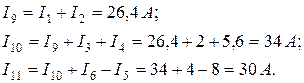
Проверим выполнение уравнения баланса мощностей источников и нагрузки:
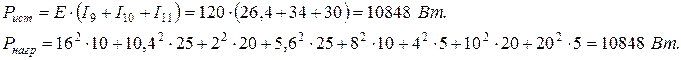
Задача 1.2.3 В электрической цепи (см. рисунок 1.4) заданы значения всех сопротивлений и ЭДС: 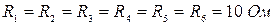 ,
, 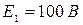 ,
, 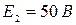 ,
, 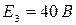 .
.
Требуется:
1) определить значения токов в ветвях электрической цепи;
2) проверить выполнение баланса мощностей источников и нагрузки.
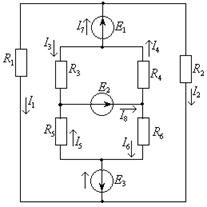
Рисунок 1.4 – Схема электрической цепи
Решение.
Преобразуем схему, заменив параллельно соединенные сопротивления одним сопротивлением, последовательно соединенные источники ЭДС одним:
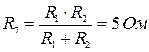 ,
, 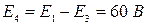 .
.
Получим эквивалентную схему, приведенную на рисунке 1.5.
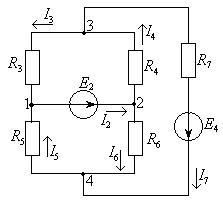
Рисунок 1.5 – Схема эквивалентной электрической цепи
Рассчитаем потенциалы узлов, используя метод узловых потенциалов:
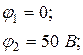
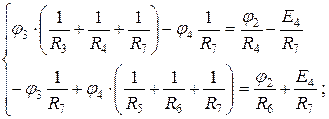
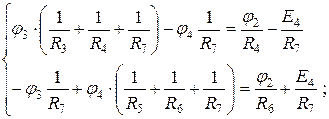
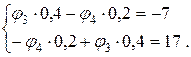
Определители системы уравнений:
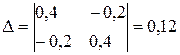 ;
; 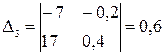 ;
; 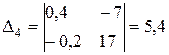 .
.
Потенциалы узлов φ 3 и φ 4:
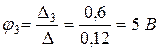 ;
; 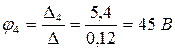 .
.
Токи в ветвях электрической цепи по закону Ома:
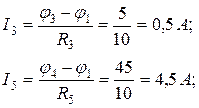
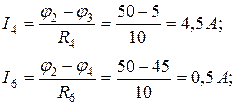
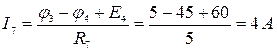 .
.
Вернувшись к первоначальной схеме, определим оставшиеся токи:
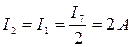 ;
; 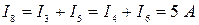 .
.
Проверим выполнение баланса мощностей источников и нагрузки:
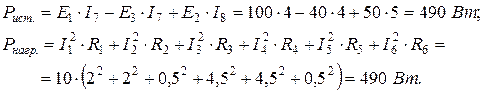
Задача 1.2.4 В электрической цепи (см. рисунок 1.6) заданы значения резисторов 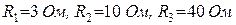 и показания амперметров
и показания амперметров 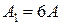 и
и 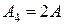 .
.
Требуется определить:
1) значения сопротивления резистора R 4 и ЭДС E;
2) значения токов в резисторах R 2 и R 3;
3) как изменить значение сопротивление резистора R 4, чтобы амперметр A 1 показал ток, равный 5 А.
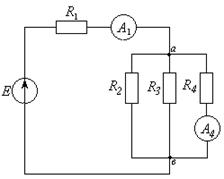
Рисунок 1.6 – Схема электрической цепи
Решение.
Заменим два параллельно соединенных сопротивления R 2 и R 3 одним эквивалентным:
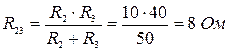 .
.
Определим сопротивление резистора R 4, используя показания амперметров, первый закон Кирхгофа и закон Ома:
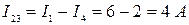 ;
; 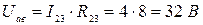 ;
;
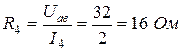 .
.
Определим значение ЭДС из уравнения по второму закону Кирхгофа:
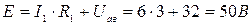 .
.
Определим токи в резисторах R 2 и R 3 по закону Ома или по формуле разброса тока по двум параллельным ветвям:
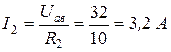 или
или 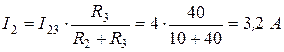 ;
;
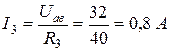 или
или 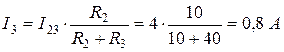 .
.
Определим эквивалентное входное сопротивление схемы, при котором амперметр A 1 покажет ток 5 А:
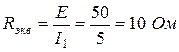 .
.
Выразим эквивалентное входное сопротивление схемы через R 4:
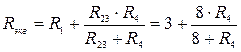 или
или 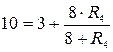 .
.
Рассчитаем значение сопротивления резистора R 4:
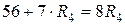 ,
, 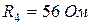 .
.
Задача 1.2.5 В электрической цепи постоянного тока, показанной на рисунке 1.7, заданы значения ЭДС и сопротивления резисторов:
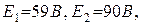
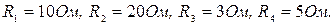
Известны также мощности, потребляемые резисторами R 1, R 3 и R 4, соответственно 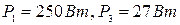 и
и 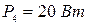 .
.
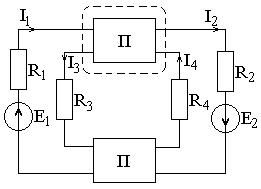
Рисунок 1.7 – Схема электрической цепи
Требуется найти мощность, потребляемую резистором R 2, если известно, что в частях схемы, заключенных в прямоугольники, источников нет.
Решение.
По известным значениям мощностей и сопротивлений резисторов можно рассчитать токи в резисторах I 1, I 3 и I 4:
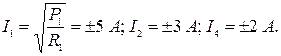
Далее запишем уравнение по первому закону Кирхгофа для показанного на рисунке 1.7 сечения схемы (при указанных направлениях токов):
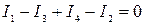 .
.
Из этого уравнения можно получить следующие возможные значения тока I 2: 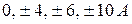 .
.
Однако 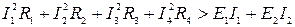 при всех значениях тока I 2, кроме значения I 2 = 4 A, т.е., только при этом значении тока I 2 выполняется баланс мощностей источников и нагрузки.
при всех значениях тока I 2, кроме значения I 2 = 4 A, т.е., только при этом значении тока I 2 выполняется баланс мощностей источников и нагрузки.
Таким образом, мощность потребляемая резистором R 2:
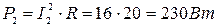 .
.
 2015-04-01
2015-04-01 3924
3924








