Непрерывная случайная величина. Функция распределения вероятностей, функция плотности распределения вероятности непрерывной случайной величины и их свойства

Интегральной функцией расnределения случайной величины Х называется функция F (x), определяющая для каждого аргумента x вероятность того, что случайная величина X принимает значения меньшие чем x, т.е. F (x) = Р (Х < х). Это вероятность того, что случайная величина X попала в интервал (-∞, x).

Свойства интегральной функции расnределения:

1. 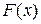не убывает (если 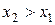, то );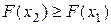

2. ;

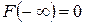3. ;

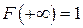4. вероятность попадания СВ X в интервале a < X < b определяется по формуле

.

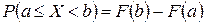Обычно для определенности левую границу включают в интервал, а правую нет. Вообще для НСВ верно, что .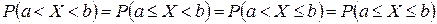

Плотностью расnределения (дифференциальной функцией распределения) непрерывной случайной величины X называется первая производная от интегральной функции распределения, т.е. функция

.

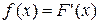Рассмотрим свойства дифференциальной функции распределения. Во-первых, плотность распределения любой случайной величины неотрицательна, т.е. f (х)³0. Во-вторых,

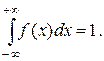
График плотности f (х) называется кривой расnределения. Второе свойство говорит о том, что площадь фигуры, образованной осью OX и кривой распределения (не всегда замкнутой) равна единице. То есть, не всякую функцию можно рассматривать в качестве функции плотности некоторой случайной величины.

Функция распределения F(х) выражается через плотность распределения формулой:

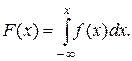
Вероятность попадания на участок от aдо b для непрерывной случайной величины выражается формулой

.

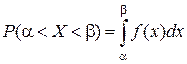Это площадь криволинейной трапеции с границами x =a, x =b, y =0, y = f (x).