2014-02-02
22233
Вычисление площадей плоских фигур
1. Площадь фигуры, ограниченной сверху графиком функции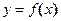 
, снизу – осью 
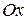, слева и справа – прямым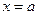и 
и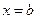 
.
Пусть функция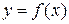 
неотрицательна и непрерывна на отрезке 
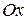. Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямым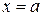и 
и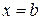 
(Рис.3) вычисляется по формуле:
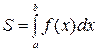. (7)
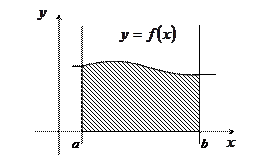
Рис. 3
Пример 11. Найти площадь фигуры, ограниченной линией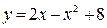 
и осью .
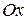Решение: Графиком функции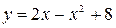 
является парабола, ветви которой направлены вниз. Построим ее (Рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью 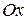(прямой 
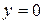). Для этого решаем систему уравнений
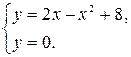
Получаем: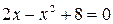 
, откуда 
, 
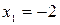; следовательно, 
, 
.
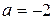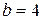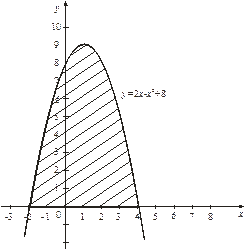
Рис. 4
Площадь фигуры находим по формуле (5):
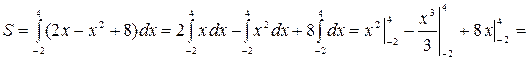
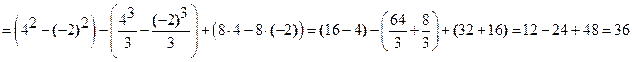(кв. ед.).
Если функция 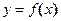неположительна и непрерывна на отрезке 
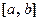, то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью 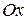, слева и справа – прямым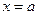и и 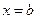, вычисляется по формуле
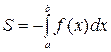. (8)
В случае если функция 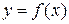непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (Рис. 4) равна алгебраической сумме соответствующих определенных интегралов:
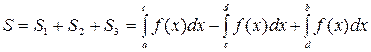. (9)
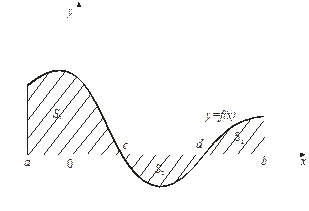
Рис. 4
Пример 12. Вычислить площадь фигуры, ограниченной осью 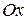и графиком функции 
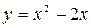при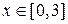 
.
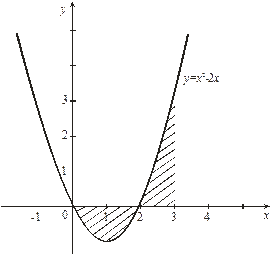
Рис. 5
Решение: Сделаем чертеж (Рис. 5). Искомая площадь представляет собой сумму площадей 
и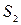 
. Найдем каждую из этих площадей. Вначале определим пределы интегрирования, решив систему 
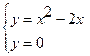. Получим 
, 
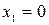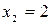. Следовательно:
;
.
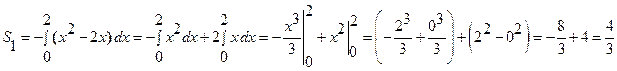Таким образом, площадь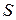 
заштрихованной фигуры равна
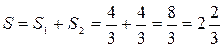(кв. ед.).
2. Площадь фигуры, ограниченной линиями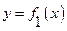 
- сверху, 
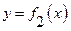- снизу, слева прямой 
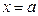, справа прямой .
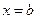Пусть, криволинейная трапеция ограничена сверху и снизу графиками непрерывных на отрезке 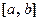функци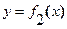й 
и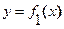 
, а слева и справа – прямым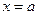и и 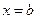(Рис. 6). Тогда ее площадь вычисляется по формуле
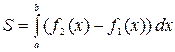. (9)
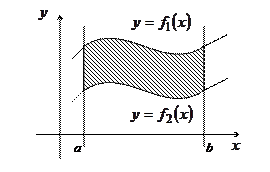
Рис. 6
Пример 13. Найти площадь фигуры, ограниченной линиям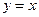и 
и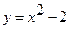 
.
Решение: Данная фигура изображена на Рис. 7. Площадь ее вычислим по формуле (8). Решая систему уравнений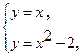 
находим 
, 
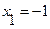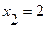; следовательно, 
, 
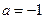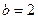. На отрезке 
имеем: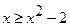 
. Значит, в формуле (7) в качестве 
возьмем x, а в качестве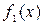 
– 
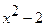. Получим:
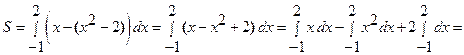
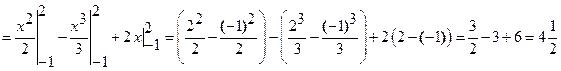(кв. ед.).
Более сложные задачи на вычисление площадей решают путем разбиения фигуры на непересекающиеся части и вычисления площади всей фигуры как суммы площадей этих частей.
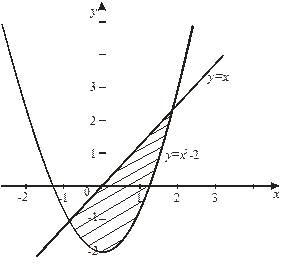
Рис. 7
Пример 14. Найти площадь фигуры, ограниченной линиями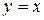 
, 
, 
.
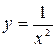
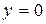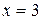Решение: Сделаем чертеж (Рис. 8). Данную фигуру можно рассматривать как криволинейную трапецию, ограниченную снизу осью 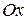, слева и справа – прямым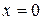и 
и 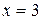, сверху – графиками функци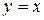й и 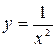. Так как фигура ограничена сверху графиками двух функций, то для вычисления ее площади разобьем данную фигуру прямой 
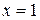на две части (1 – это абсцисса точки пересечения лини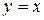й и 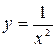). Площадь каждой из этих частей находим по формуле (4):
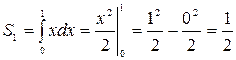(кв. ед.);
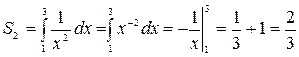(кв. ед.). Следовательно:
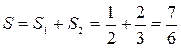(кв. ед.).
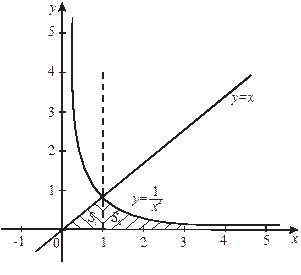
Рис. 8
Если криволинейная трапеция ограничена прямым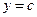и 
и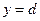 
, осью 
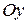и непрерывной на 
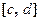кривой
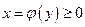(Рис. 9), то ее площадь находится по формуле
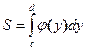. (10)
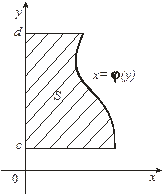
Рис. 9
