Пример 1.5

Один рабочий обслуживает три станка. Станок останавливается в среднем 2 раза в час, наладка станка занимает около 10 минут. Определить:

- вероятность того, что рабочий занят ;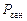

- коэффициент занятости системы .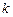

Определим основные характеристики СМО (СМО является замкнутой)

,

,

,

,

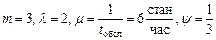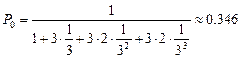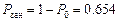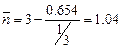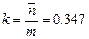— около 35% станков простаивают из-за поломок.

1.14 СМО с ограниченным временем ожидания

Рассмотрим вариант многоканальной СМО с ограниченным временем ожидания. Заявки, поступающие на вход системы и заставшие все каналы обслуживания занятыми, встают в очередь. По количеству мест очередь не имеет ограничений. Но заявка, простоявшая некоторое время в очереди и не получившая обслуживание, покидает очередь с интенсивностью ухода 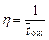(например, покупателю надоело стоять в очереди в магазине и он уходит; позвонив по телефону и услышав «занято», человек какое-то время ждет, а затем бросает трубку и т.д.). Будем считать, что время ожидания распределено экспоненциально со средним .

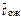Построим граф переходов для данной системы:

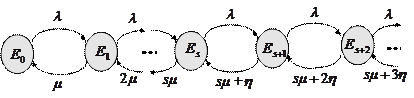Рисунок 1.13 – Граф переходов

Уравнения вероятностей состояний

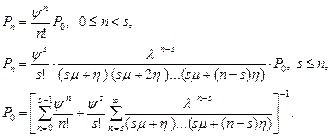
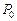вычисляется приближенно (ряд не является геометрической прогрессией). Здесь стационарный режим существует всегда: ряд 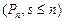сходится. Вероятность отказа для данной системы не имеет смысла.

Среднее количество заявок в очереди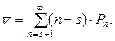

Абсолютная пропускная способность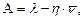

где 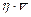— заявки, ушедшие из очереди в единицу времени.

Тогда относительная пропускная способность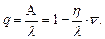

Среднее число занятых каналов 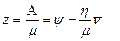или

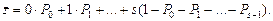
Тогда среднее количество заявок в очереди можно найти по формуле

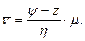
2 Сети СМО

2.1 Общие сведения о сетях СМО

В общем случае сеть СМО можно представить в виде графа, вершинами которого являются одноканальные и многоканальные СМО (дуги определяют потоки передачи требований).

Простейшая разомкнутая или открытая сеть получается при по­следовательном соединении СМО (рисунок 2.1). Она еще называется многофазной СМО.

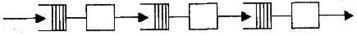
Рисунок 2.1 – Открытая сеть

Различают замкнутые и разомкнутые сети. Для замкнутой веро­ятностной сети не существует внешних источников требований, то есть в ней всегда находится одно и то же количество требований. Для разомкнутой сети имеются источники требований и стоки требований.

Простейшая замкнутая сеть показана на рисунке 2.2. Эта система с отказами и восстановлениями хорошо известна из теории массового обслуживания. В системе постоянно находятся М требований, кото­рые появляются при отказе устройств М. Если устройство отказало, то поступает требование на его ремонт к бригаде с N ремонтниками, которые ремонтируют устройство, а потом отремонтированное уст­ройство восстанавливает свою работу. На рисунке 2.2 это показано об­ратной связью от N устройств. Сеть также используется при модели­ровании компьютерной системы, которая работает в режиме «запрос - ответ», то есть пользователь не посылает новый запрос к системе до тех пор, пока не получит ответ на предшествующий запрос. За­просы обрабатываются любым из N компьютеров. Примерами таких систем могут быть автоматизированные системы продажи билетов на поезда или самолеты, системы передачи транзакций от кассиров в банке и т. п.

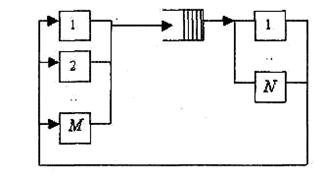
Рисунок 2.2 – Замкнутая сеть

Сеть (рисунке 2.3) содержит К узлов и N требований, которые нахо­дятся в сети. Каждый узел может иметь одно или несколько одинако­вых устройств обслуживания. С вероятностью (или частотой) q_0j тре­бования поступают к любому узлу сети, а с вероятностью q_kj (j = 1,..., К) требование, которое оставляет узел k, направляется к узлу j. Таким образом, любое требование до завершения своего обслужи­вания в сети обычно проходит несколько узлов.

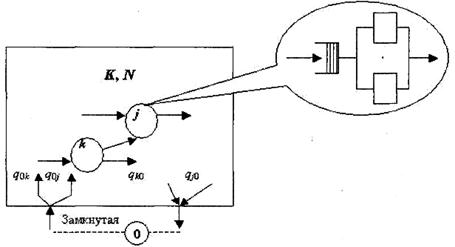
Рисунок 2.3 – Сеть из К узлов

Внешняя среда обозначается как узел 0 сети. Если сеть замкну­тая, то требования с выхода направляются на вход (рисунке 2.3, пунктир­ная линия), и количество требований N в сети не изменяется.

Для потоков требований в сети справедливы законы о суммар­ных потоках, которые показаны на рисунках 2.4, 2.5, при условии, что сеть работает в установившемся режиме.

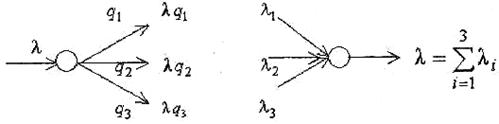
Рисунок 2.4 - РазъединениеРисунок 2.5 - Соединение

Для расчетов сетей массового обслуживания используется теория вероятностных сетей, которая основывается на марковских и полумарковских процессах, но большинство результатов получено только для экспоненциальных законов распределения. При количестве узлов сети больше трех для расчетов используются численные приближенные методы. Операционный анализ в отличие от тео­рии массового обслуживания опирается на логику работы рассматри­ваемой или моделируемой системы. Это позволяет установить про­стые зависимости между параметрами и показателями работы систе­мы, не абстрагируясь от процессов ее функционирования.

2.2 Операционный анализ вероятностных сетей

Операционный анализ вероятностных сетей базируется на сле­дующих принципах:

- все предположения относительно операционных переменных
можно проверить измерениями на реальной системе или на ее
модели;

- в системе должен существовать баланс потоков: количество
требований, которые покинули систему за некоторый период
наблюдения, должно равняться количеству требований, которые поступили в систему за этот же период;

- переходы требований от одного узла к другому не должны зависеть от длин очередей в узлах.

Таким образом, рассматриваемая система должна работать в установившемся, а не в переходном режиме.

Основная задача операционного анализа вероятностных сетей состоит в определении таких показателей, как среднее время пребывания требований в отдельных узлах сети, загрузка устройств в узлах, средние длины очередей к узлам и т.п.

Большинство результатов операционного анализа касается замкнутых сетей, когда требования, которые покидают сеть, снова возвращаются в нее. Замкнутые сети можно использовать, когда рас­сматриваемая система работает с перегрузкой. В этом случае можно считать, что вместо требования, которое покинуло систему, в систему поступает другое требование с такими же параметрами.

Введем операционные переменные, которые можно получить или измерениями, или в процессе имитационного моделирования системы:

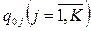-вероятность (частота) поступления требований в сеть извне к любому узлу (К - общее количество узлов);

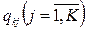- вероятность перехода требований из узла k к узлу j

;

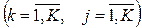q_k0 - вероятность того, что после окончания обслуживания в узле к требования покинут сеть;

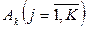- количество требований, которые поступили в узел k;

С _kj 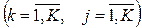- количество требований, которые покинули узел k и поступили в узел j;

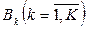- общее время обслуживания требований узлом k;

Т - общее время наблюдения за системой или время моделиро­вания.

Внешнюю среду обозначим как вершину с номером 0. Тогда A_0j, C_k0 будут приобретать значения количества требований, которые поступили в узел j, и требований, которые покинули узел k, соответ­ственно.

Узел считается занятым, если в нем есть хотя бы одно требова­ние. Введем дополнительные обозначения

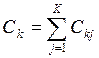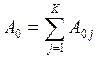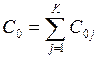, , . (2.1)

Для замкнутой сети А₀ = С₀.

Введенные переменные называются основными операционны­ми переменными. Используя эти переменные и выполняя простейшие операции над ними, получают выводимые операционные пере­менные. Наиболее часто используют такие

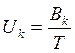,(2.2)

где U_k - коэффициент использования узла;

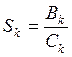,(2.3)

где S_k- среднее время обслуживания в узле k;

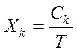,(2.4)

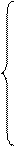
где Х_k - интенсивность выходящего потока требований из узла 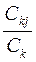k;

, k =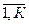

q_kj =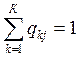

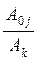, k=0,

где q_kj - относительная частота перехода требований между узлами k и j Используя выражения (2.2 – 2.4), имеем:

U_k=X_kS_k (2.6)

2.3 Операционные зависимости

Основные результаты операционного анализа формулируются в виде соотношений между операционными переменными. Основой этих соотношений является гипотеза о балансе потоков в сети: коли­чество требований, которые поступили в некоторый узел на протяжении продолжительного периода Т, равняется количест­ву требований, которые покинули этот узел. Эта гипотеза опреде­ляет работу сети СМО в установившемся режиме, то есть требования всегда покидают узлы сети.

Гипотеза о балансе позволяет установить зависимости между операционными переменными для каждого узла сети. Эта гипотеза позволяет записать уравнения баланса потоков

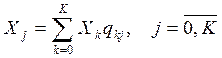. (2.7)

Справедливость выражения (2.7) вытекает из предположения о балансе потоков в сети, то есть A_j = C_j, так как 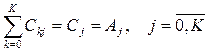но при условии, что q_kj = 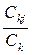, находим С_j = 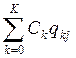. Поделив последнее соотношение (левую и правую его части) на общее время наблюде­ния Т, получим выражение (2.7). Уравнения (2.7) будут иметь единст­венное решение для замкнутой сети при заданном х₀. Для разомкну­той сети уравнения (2.7) будут линейно зависимыми, однако, и в этом случае они имеют полезную информацию о динамике потоков сети. Найдем из выражения (2.6) производительность узла

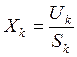. (2.8)

Определим коэффициент посещаемости узла k

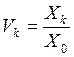. (2.9)

Уравнение баланса потока можно представить в эквивалентной системе, в которой вместо интенсивности потоков используются коэффициенты посещаемости каждого узла сети.

Поделим левую и правую части выражения (2.7) на Х_о

V₀ = 1, V_j = q_oj + 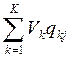, 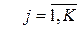. (2.10)

Выражения (2.10) справедливы, если справедливы уравне­ния (2.7), поскольку (2.10) получены из (2.7).

Связь коэффициентов посещаемости и производительности узла определяем по формуле

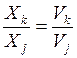. (2.11)

Для определения среднего времени пребывания требования в вероятностной сети обозначим это время через R, а для отдельных узлов - через R_k. Введем еще одну операционную переменную - W_k, которая равняется суммарному времени ожидания и времени обслу­живания требования узлом k на протяжении времени Т

N

= у Пк

(2.19)

к=\Хк

^0 4=1

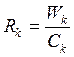. (2.12)

Среднее время пребывания в системе можно найти через R_k и коэффициенты посещаемости отдельных узлов, то есть

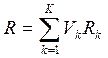. (2.13)

Это общий закон времени пребывания, который справедлив и в том случае, если гипотеза о балансе потоков не выполняется.

Среднее количество требований в сети N, которое определяется через среднее количество требований в каждом узле п_k, равно

N= 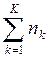, (2.14)

где n_k — выводимая операционная переменная, которую можно получить из основных операционных переменных

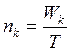. (2.15)

Для среднего времени пребывания требований в сети справед­лив закон Литтла: среднее время пребывания в устройстве k опре­деляется через среднее количество требований в устройстве и интен­сивность потока

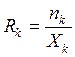. (2.16)

Обосновать формулу Литтла можно с помощью операционного анализа. Из выражения (2.15) находим

W_k = n_k T. (2.17)

Подставляем полученную операционную переменную в уравне­ние (2.12)

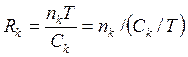
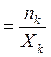. (2.18)

Закон Литтла справедлив также для всей сети в целом. Подста­вим выражение для V_k из уравнения (2.9) в (2.13) и выражение для R_k из (2.16), тогда

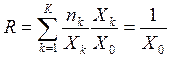
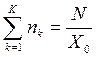. (2.19)

Покажем, как можно использовать операционный анализ для определения времени пребывания в замкнутой сети (рисунок 2.6).

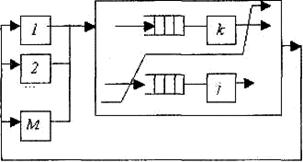
Рисунок 2.6 – Замкнутая сеть

Пусть есть М устройств, время обслуживания требования лю­бым из них - Z. Среднее время пребывания требования в сети опре­деляем по формуле

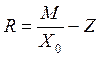. (2.20)

Выражение (2.20) получено из таких соображений. Среднее время одного цикла взаимодействия, включая время обслуживания требования во внешней сети и пребывание в одном из М устройств, определяется суммой Z + R. Если предположить, что выполняется ги­потеза о балансе потоков, то для рассматриваемого цикла справедли­ва формула Литтла. Поэтому величина (Z + R)X₀ должна определять среднее количество занятых устройств или среднее количество рабо­тающих устройств для системы с отказами. Таким образом, общее количество устройств

M = (Z + R)X₀. (2.21)

Продемонстрируем использование приведенных соотношений операционного анализа на примерах.

Пример 2.1. Пусть имеем М= 20 устройств. Среднее время обслуживания каждым Z = 25 с (рис. 2.7).

Для узлов l, g, n сети частоты перехода к узлу t равняются соответственно: q_lt = 0,5; q_mt = 0,7; q_nt =0,85, а коэффициенты посещаемо­сти этих узлов равняются V_l =12; V_g =17; V_n =19. Узел t используется на 50%, среднее время обслуживания узлом t поступающих требова­ний составляет 25 мс. Необходимо найти среднее время пребывания и среднее количество требований в сети.

Определим коэффициент посещаемости узла t, используя урав­нения баланса потоков (2.10), записанные через коэффициенты посе­щаемости узлов

V_t = V_l q_lt + V_g q_gt + V_n q_nt,

V_t = 12 · 0,5 + 17 · 0,7 + 19 · 0,85 = 34,05.

Находим интенсивность поступления требований в сеть

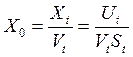. (2.22)

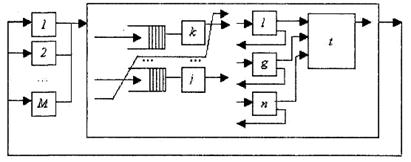
Рисунок 2.7 – Фрагмент сети

В выражение (2.22) входят известные из условий операционные переменные: U_t = 50% и S_t = 0,025 с. Следовательно, получим

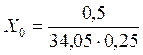= 0,587 требований/с.

Из выражения (2.19) находим время пребывания требования в сети

R = 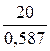- 25 = 9,072 с.

Для определения среднего количества требований в сети вос­пользуемся формулой Литтла

N = RX₀,

N = 9,072 · 0,587 = 5,33 требований.

Пример 2.2. Рассмотрим сеть, в которую поступают требова­ния как из обслуживающих устройств (замкнутая часть сети), так и извне (рисунок 2.8).

Есть М = 40 обслуживающих устройств. Среднее время обслу­живания каждым Z = 15 с. В результате проведенных исследований получены такие данные о сети:

- среднее время пребывания требований, которые поступают от 40
устройств обслуживания в сеть, равняется 5 с;

- среднее время обслуживания любого требования узлом t составляет 40 мс;

- каждое требование, которое поступает от М устройств
обслуживания, порождает 10 требований к узлу t;

- каждое требование, которое поступает в систему извне, порож­дает 5 требований к узлу t;

- узел t используется на 90%.

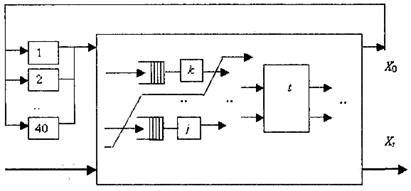Рисунок 2.8 – Фрагмент сети

Нужно определить нижнюю границу времени пребывания в сети требований, которые поступают от М устройств обслуживания с интенсивностью входящего потока Х₀ и от внешнего источника требо­ваний в сеть с интенсивностью X_t, что выходят из узла t.

При решении поставленной задачи переменные, которые каса­ются поступающих от М устройств обслуживания требований, будем обозначать звездочкой.

Из выражения (2.20) для потока требований от М устройств на­ходим

,

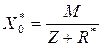где Z- среднее время обслуживания М устройствами; R* - среднее время пребывания требований, которые поступили от 40 устройств обслуживания в сеть. Тогда

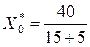= 2 требования/с.

Интенсивность потока требований в узел t определяем как сумму

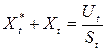(2.24 )

интенсивности потоков требований от устройств обслуживания и интенсивности потока внешних требований, то есть 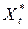+ X_t. Тогда в соответствии с выражением (2.3.1) можно записать

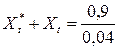= 22,5 требований/с.

Используя формулу для коэффициента посещаемости (2.8), на­ходим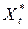

= ,

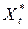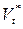
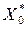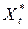=10·2 = 20 требований/с,

отсюда,

X_t = 2,5 требований/с.

Теперь можно найти интенсивность Х₀ входящего потока внеш­них требований в сеть

,

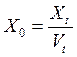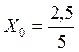= 0,5 требований/с.

Допустим, что исходные условия изменились и интенсивность входящего потока внешних требований увеличилась втрое, то есть Х₀ = 1,5 требований/с. Тогда X_t = V_tX₀ = 1,5 требований/с. Считая, что среднее время обработки требований узлом t не изменилось, получа­ем, что максимально возможная интенсивность обслуживания требований узлом t, составляет 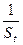= 25 требований/с при 100% использовании узла t. Таким образом, интенсивность обслуживания требований узлом t от устройств обслуживания не может превышать

25 - 7,5 = 17,5 требований/с.

Исходя из этого,

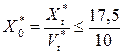= 1,75 требований/с.

Итак, нижняя граница времени пребывания в сети требований, которые поступают от 40 устройств обслуживания в соответствии с выражением (2.19)

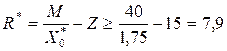с.

Таким образом, увеличение в три раза интенсивности потока внешних требований приведет к увеличению среднего времени пре­бывания требований в сети от 40 устройств обслуживания на 2,9 с.

3 Система имитационного моделирования GPSS

3.1 Имитационное моделирование

Имитационное моделирование процессов обслуживания вызовов универсальный и в некоторых случаях единственно возможный способ математического моделирования систем телекоммуникаций. Он применяется в том случае, когда не удается определить характеристики качества обслуживания и другие количественные оценки аналитическим или численным методом, либо когда найденное решение требует уточнения.

При моделировании имитируется работа системы коммутации и собирается, обрабатывается и выдается необходимая статистика об имитируемом процессе.

По сравнению с непосредственным экспериментом на станции или сети связи моделирование на ЭВМ обладает рядом преимуществ: его можно применить к новым, еще не разработанным системам распределения информации; работу исследуемой систему можно проверить в самых разнообразных условиях.

Итак, имитационное моделирование в области телекоммуникаций применяется, в основном, в следующих трех случаях:

1) при исследовании системы коммутации или сети связи; для определения пропускной способности, характеристик качеств обслуживание;

2) при проектировании; можно определить структурные оптимальные параметры, апробировать алгоритмы;

3) при создании обучающих тренажеров.

Моделирование начинается с разработки задания на его проведение. В нем формируют цель и задачи исследования на компьютере, определяют требования к точности и объему получаемых результатов, подробно описывают все элементы изучаемой модели: структуру системы коммутации, и ее изменяемые параметры, модель потока вызовов, дисциплину обслуживание и выводимые статистические характеристики.

По материалам задания разрабатывается алгоритм и составляется программа. Поскольку алгоритм моделирования должен отражать случайную природу имитируемого процесса, то в его реализации используются случайные числа и события.