Умножение на четыре разряда одновременно

В этом случае с помощью приема, аналогичного приему, использованному в случае умножения на два разряда одновременно, можно рассматривать сразу тетраду двоичных разрядов. Может быть выведено общее правило сокращенного умножения:

1. Если цифра множителя b_i-1 < r/2, то 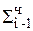+ 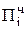, где 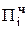= Мн b_i.

2. Если цифра множителя b_i-1 ³ r/2, то 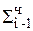+ 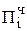, где 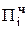= [Мн (r - b_i)]_доп.

Анализ четырех двоичных разрядов одновременно дает возможность осуществить сдвиг на четыре разряда за один такт.

Пример: Мн = 011

Мт = С49

Мт^п = 1457

Можно заранее заготовить кратные множители: Мн, 2Мн, 4Мн, поместив их в дополнительные регистры. Это позволит сократить время, необходимое для формирования частичного произведения 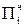, равного от нуля до семи множимых.

[+7Мн]_доп = 0.10101 [+5Мн]_доп= 0.01111 [+4Мн]_доп= 0.01100

[-7Мн]_доп = 1.01011 [-4Мн]_доп = 1.10100

0.00000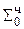

⁺ 1.01011 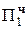= -7Mн

1.01011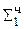

1. 1111 0 1011 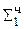∙ 2^-4

⁺ 0.01111 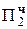= +5Mн

0.01101 1011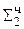

0. 0000 0 1101 1011 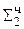∙ 2^-4

⁺ 1.10100 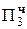=-4Mн

1.10100 1101 1011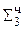

1. 1111 1 0100 1101 1011 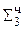∙ 2^--4

⁺ 0.00011 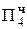= +Mн

0.00010 0100 1101 1011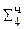

0. 0000 00010 0100 1101 1011 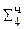∙ 2^--4 = Мн∙Мт