2015-04-01
681
Преобразования Лапласа. Операторный метод расчёта переходных процессов широко применяется в теории электрических цепей для решения линейных дифференциальных и интегро-дифференциальных уравнений
Суть операторного метода заключается в том, что функции f(t) действительной переменной t сопоставляется функция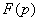 
комплексной переменной 
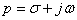. Это сопоставление осуществляется с помощью прямого преобразования Лапласа:
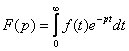. (2.1)
Функция f(t) называется оригиналом, функция 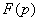называется изображение. Это сопоставление обозначается: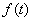 
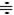
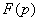и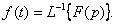 
Из выражения (2.1) следует, что изображение постоянной равно: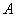 
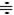
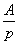. Изображения производных: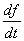 
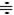
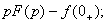
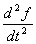
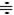
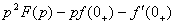где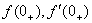 
− начальные значения функции и её производной. При нулевых начальных значениях 
: 
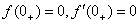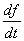
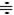
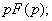
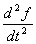
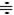
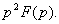
Изображение интеграла: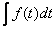 
.
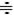
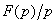Таким образом изображения производных и интегралов от оригинала выражаются алгебраическими функциями от изображения и от начальных значений самой функции и её производных. Отсюда следует, что система интегро-дифференциальных уравнений относительно оригиналов заменяется системой алгебраических уравнений относительно их изображений. При этом нет необходимости вычислять постоянные интегрирования.
|
|
|
