Оригинал 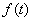 можно определить по его изображению
можно определить по его изображению 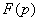 , используя таблицы, обратное преобразование Лапласа, теорему разложения.
, используя таблицы, обратное преобразование Лапласа, теорему разложения.
Таблица 2.1-Теорема разложения
Изображение имеет вид рациональной дроби: 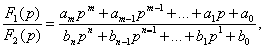 где m<n, где m<n,  - характеристическое уравнение. Оригинал определяется по теореме разложения. - характеристическое уравнение. Оригинал определяется по теореме разложения. | |
по вид корней характеристического уравнения  | Теорема разложения |
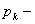 простые вещественные корни характеристического уравнения простые вещественные корни характеристического уравнения  | 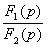 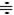 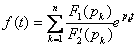 где где 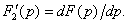 |
знаменатель имеет один нулевой корень: 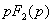 | 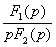 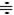 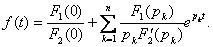 |
1. характеристическое уравнение  имеет простые вещественные корни имеет простые вещественные корни 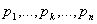 и комплексные сопряженные корни и комплексные сопряженные корни 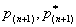 . . | 1. 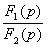 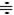 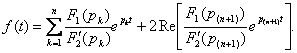 |
Продолжение таблицы 2.1
2. 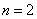 , , 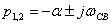 - комплексные сопряженные корни уравнения - комплексные сопряженные корни уравнения  | 2. 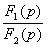 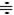 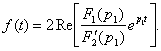 |
 2015-04-01
2015-04-01 789
789








