Непрерывные цепи Маркова

Марковский случайный процесс с дискретными состояниями и непрерывным временем называется непрерывной цепью Маркова при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.

Часто встречаются ситуации, которые указать заранее невозможно. Например, любая деталь или агрегат могут выходить из строя в любой, непредсказуемый заранее момент времени. Для описания таких систем и отдельных случаев можно использовать математический аппарат непрерывной цепи маркова.

Пусть система характеризуется n состояниями S₁, S₂, …, S_n, а переход из состояния в состояние может осуществляться в любой момент времени. Обозначим через P_i(t) вероятность того, что в момент времени t система S будет находиться в состоянии S_i (i = 1, 2,..., n). Требуется определить для любого t вероятности состояний P₁(t), P₂(t), …, P_n(t). Очевидно, что

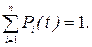
Для процесса с непрерывным временем вместо переходных вероятностей P_ij рассматриваются плотности вероятностей перехода l_ij, представляющие coбой предел отношения вероятности перехода системы за время Dt из состояния S_i в состояние S_j к длине промежутка Dt:

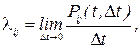(3.2)

где P_ij(t, Dt) – вероятность того, что система, пребывавшая в момент t в состоянии S_i, за время Dt перейдет из него в состояние S_j (при этом всегда i ¹ j).

Если l_ij = const, то процесс называется однородным, если плотность вероятности зависит от времени l_ij = l_ij(t), то процесс - неоднородный.

При рассмотрении непрерывных марковских процессов принято представлять переходы системы S из состояния в состояние как происходящие под влиянием некоторых потоков событий.

Плотность вероятности перехода интерпретируется как интенсивность l_ij соответствующих потоков событий. Если все эти потоки пуассоновские, то процесс, протекающий в системе S, будет марковским.

При изучении марковских случайных процессов с дискретными состояниями и непрерывным временем в графе состояний над стрелками, ведущими из состояния S_i в S_j, проставляют соответствующие интенсивности l_ij. Такой граф состояний называют размеченным.

Пусть система S имеет конечное число состояний S₁, …, S_n. Случайный процесс, протекающий в этой системе, описывается вероятностями состояний P₁(t), …, P_n(t), где P_i(t) - вероятность того, что система S в момент t находится в состоянии S_i. Для любого t

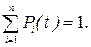
Вероятности состояний Р_i(t) находят путем решения системы дифференциальных уравнений (уравнении Колмогорова), имеющих вид

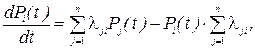(3.3)

где i = 1, 2, …, n.

Величина l_ijP_ij(t) называется потоком вероятности перехода из состояния S_i в S_j, причем интенсивность потоков l_ij может зависеть от времени или быть постоянной.

Уравнения (3.3) составляют по размеченному графу состояний системы, пользуясь следующиммнемоническим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное состояние, минус сумма всех потоков вероятности, идущих из данного состояния в другие.