При решении многих практических задач не всегда нужно характеризовать случайную величину полностью, т. е. определять законы распределения. Кроме того, построение функции или ряда распределений для дискретной, а плотности - для непрерывной случайной величины громоздко и излишне.
Иногда достаточно указать отдельные числовые параметры, частично характеризующие особенности распределения. Необходимо знать некоторое среднее значение каждой случайной величины, около которого группируется ее возможное значение, или степень разбросанности этих значений относительно среднего и т. п.
Характеристики наиболее существенных особенностей распределения называются числовыми характеристиками случайной величины. С их помощью облегчается решение многих вероятностных задач без определения для них законов распределения.
Важнейшей характеристикой положения случайной величины на числовой оси является математическое ожидание М [ X ] = а, которое иногда называется средним значением случайной величины. Для дискретной случайной величины X с возможными значениями x 1, x 2, …, xn и вероятностями p 1, p 2, …, pn его определяют по формуле
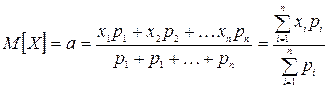 .
.
Учитывая, что 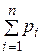 =1, можно записать
=1, можно записать
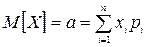 .
.
Таким образом, математическим ожиданием дискретной случайной величины называется сумма произведений возможных ее значений на их вероятности. Среднее арифметическое значение наблюдаемых значений случайной величины при большом числе опытов приближается к ее математическому ожиданию.
Для непрерывной случайной величины X математической ожидание определяется не суммой, а интегралом
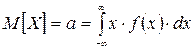 ,
,
где f (x) — плотность распределения величины X.
Математическое ожидание существует не для всех случайных величин. Для некоторых из них сумма, или интеграл, расходится, и, следовательно, математического ожидания не существует. В этих случаях по соображениям точности следует ограничивать область возможных изменений случайной величины X, для которых сумма, или интеграл, будут сходиться.
На практике применяются и такие характеристики положения случайной величины, как мода и медиана.
Модой случайной величины называется ее наиболее вероятное значение. В общем случае мода и математическое ожидание не совпадают.
Медианой случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины, т. е. это абсцисса точки, в которой ограниченная кривой распределения площадь делится пополам. Для симметричного распределения все три характеристики совпадают.
Кроме математического ожидания, моды и медианы в теории вероятностей используются и другие характеристики, каждая из которых описывает определенное свойство распределения. Например, числовыми характеристиками, характеризующими рассеивание случайной величины, т. е. показывающими, насколько тесно сгруппированы ее возможные значения около математического ожидания, являются дисперсия и среднее квадратическое отклонение. Они существенно дополняют случайную величину, так как в практике часто встречаются случайные величины с равными математическими ожиданиями, но различными распределениями. При определении характеристик рассеивания используют разность между случайной величиной X и ее математическим ожиданием, т. е.
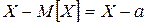 ,
,
где а = М [ X ] — математическое ожидание.
Эта разность называется центрированной случайной величиной, соответствующей величине X, и обозначается 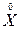 :
:
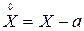 .
.
Дисперсия случайной величины - это математическое ожидание квадрата отклонения величины от ее математического ожидания, т. е.:
D[ X ]=M[(X – a)2], или
D[ X ]=M[ 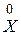 2].
2].
Дисперсия случайной величины является удобной характеристикой рассеивания и разбросанности значений случайной величины около ее математического ожидания. Однако она лишена наглядности, так как имеет размерность квадрата случайной величины.
Для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Такой величиной является среднее квадратическое отклонение случайной величины, которое представляет собой положительный квадратный корень из ее дисперсии.
Математическое ожидание, мода, медиана, дисперсия, среднее квадратическое отклонение - наиболее часто используемые числовые характеристики случайных величин. При решении практических задач, когда невозможно определить закон распределения, приблизительным описанием случайной величины являются ее числовые характеристики, выражающие какое-либо свойство распределения.
Кроме основных характеристик распределения центра (математического ожидания) и рассеивания (дисперсии) часто нужно описать другие важные характеристики распределения - симметрию и островершинность, которые можно представить с помощью моментов распределения.
Распределение случайной величины, полностью задано, если известны все его моменты. Однако многие распределения можно полностью описать с помощью первых четырех моментов, которые являются не только параметрами, описывающими распределения, но имеют также важное значение при подборе эмпирических распределений, т. е. вычислив числовые значения моментов для заданного статистического ряда и, использовав специальные графики, можно определить закон распределения.
В теории вероятностей различают моменты двух видов: начальные и центральные.
Начальным моментом k-го порядка случайной величины Т называют математическое ожидание величины Xk, т. е.
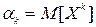 .
.
Следовательно, для дискретной случайной величины он выражается суммой
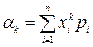 ,
,
а для непрерывной – интегралом
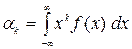 .
.
Среди начальных моментов случайной величины особое значение имеет момент первого порядка, который является математическим ожиданием. Начальные моменты высших порядков используются, главным образом, для вычисления центральных моментов.
Центральным моментом k-го порядка случайной величины называют математическое ожидание величины (X - М [ X ]) k
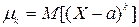 ,
,
где а = М [X].
Для дискретной случайной величины он выражается суммой
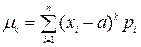 ,
,
а для непрерывной – интегралом
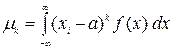 .
.
Среди центральных моментов случайной величины особое значение имеет центральный момент второго порядка, который представляет дисперсию случайной величины.
Центральный момент первого порядка всегда равен нулю.
Третий начальный момент характеризует асимметрию (скошенность) распределения и по результатам наблюдений для дискретной и непрерывной случайных величин определяется соответствующими выражениями:
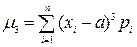 ;
; 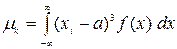 .
.
Поскольку он имеет размерность куба случайной величины, то, чтобы получить безразмерную характеристику, m3 делят на среднее квадратическое отклонение в третьей степени
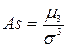 .
.
Полученная величина называется коэффициентом асимметрии и в зависимости от знака характеризует положительную (As > 0) или отрицательную (As < 0) скошенность распределения (рис. 2.3).
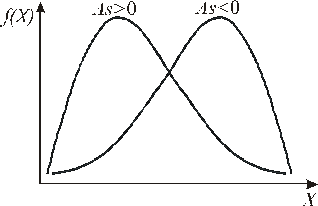 | Рис. 2.3. Кривые с положительным и отрицательным эксцессом |
Четвертый центральный момент m4 характеризует островершинность или плосковершинность распределения и для дискретных и непрерывных случайных величин определяется соответствующими выражениями:
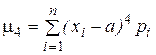 ;
; 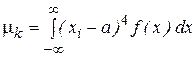 .
.
Однако на практике эти свойства распределения описываются с помощью безразмерной характеристики, называемой эксцессом
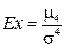 .
.
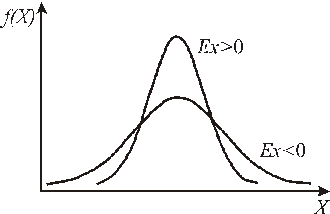 | Рис. 2.4. Кривые нормального распределения с положительным и отрицательным эксцессом |
Кривая нормального распределения с эксцессом, равным нулю, является как бы эталоном, с которым сравнивают другие распределения.
Более островершинные кривые имеют положительный эксцесс, а более плосковершинные - отрицательный.
Таблица
Функции распределения наиболее распространенных законов
| Вид графика | Название и функция распределения закона |
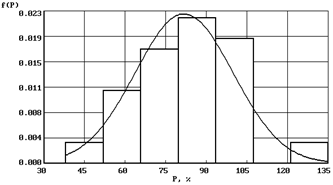 | Нормальный закон (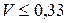 ) ) 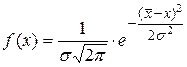 |
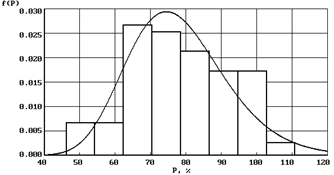 | Логнормальный закон (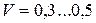 ) ) 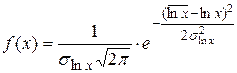 |
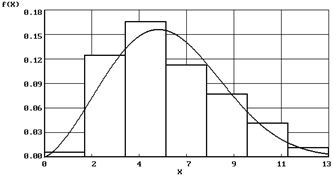 | Закон Вейбулла (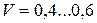 ) ) 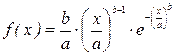 |
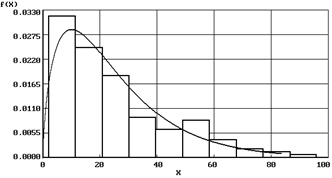 | Гамма- закон (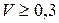 ) ) 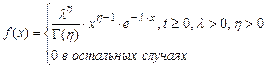 |
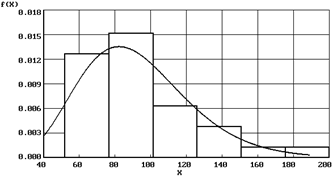 | Закон Эрланга (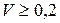 ) ) 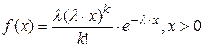 |
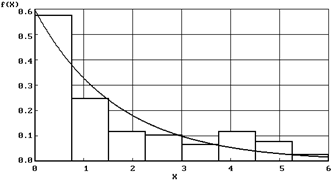 | Экспоненциальный закон (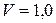 ) ) 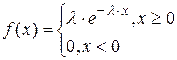 |
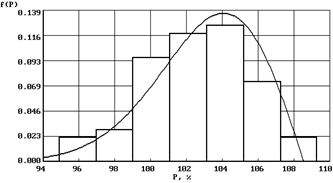 | ТР-закон (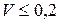 ) ) 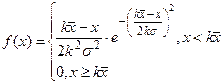 ; ; 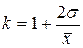 |
 2015-04-01
2015-04-01 16419
16419
