Слабоустойчивые совместные решения по Ю. Б. Гермейеру

Пусть задана исходная игра

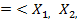
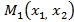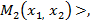
Г , 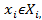i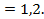

Для этой игры определим следующие величины (минимаксные выигрыши):

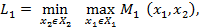
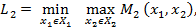
Введем стратегии наказания:

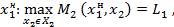
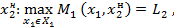
И определим множества:

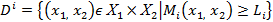, i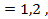

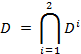
Множество D – взаимовыгодное множество, при выборе управления из этого множества игроки получают выигрыш, не меньший, чем их минимаксный результат.

Пусть 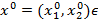D - совместный выбор, являющийся результатом неформального компромисса.

Введём обозначения:

,

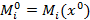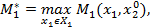
Замечание 1. Очевидно, имеет место цепочка неравенств:

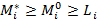
Определение. Ситуация 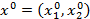называется слабоустойчивым совместным решением по Ю. Б. Гермейеру, если выполняются неравенства

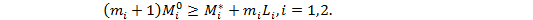(1)

Таким образом, построение устойчивой ситуации проводится при условии дальнейшего повторения игры, что приводит к возможности наказания игрока, отклонившегося от выбора, соответствующего равновесной ситуации.

Полученное решение состоит из двух компонент:

1) Стационарное решение ;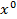

2) Реализация минимума функции 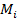в последующих 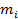повторениях, если игрок 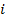нарушил соглашение по выбору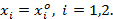

При этом предполагается, что результаты предыдущих повторений становятся известными к следующему повторению, а выигрыши игроков определяются в виде суммы выигрышей в 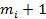повторениях игры.

Замечание 2. В случае 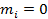получаем классическое определение ситуации равновесия по Нэшу:

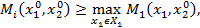
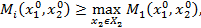
Замечание 3. Так как 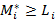, то из определения 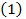получим

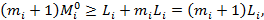
то есть 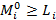, i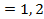

Следовательно 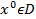,то есть компромиссное решение может быть выбрано только из взаимовыгодного множества.