Численными называется методы решения задачи, реализуемые с помощью последовательных приближений. Все эти методы подразделяются на два класса:
1. Методы не использующие производных.
2. Методы использующие производные.
К первой группе относятся:
1. Метод перебора.
2. Метод поразрядного поиска.
3. Методы исключения отрезков.
4. Метод парабол.
Метод перебора заключается в простом переборе всех вариантов и поиске оптимальных значений. Эффективно когда переменная является дискретной, а вариантов не очень много.
Метод поразрядного поиска заключается в том, что весь интервал значений переменных, разбивается точками на отрезки или разряды, затем методом перебора определяется точка, где функция минимальна, после этого прилегающие к этой точке отрезки, вновь разбиваются на разряды, но уже более мелкие, и снова ищутся точки с минимумом функции. Это повторяется до тех пор, пока ширина разрядов не станет меньше требуемой точности расчёта.
Методы исключения отрезков заключаются в том, что на всём интервале переменной выбираются две пробных промежуточных точки и значением целевой функции в этих точках отбрасывается та часть отрезка, где заведомо нет минимума. Наиболее эффективным способом исключения отрезков является метод золотого сечения.
Метод парабол состоит в том, что целевая функция по трём избранным точкам аппроксимируется параболой и за счёт этого пошагово находится минимум.
Метод золотого сечения.
Предположим, что необходимо найти минимум функции f(x), на отрезке 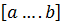 , причём известно, что функция унимодальна. На выбранном отрезке намечаются две пробных точки
, причём известно, что функция унимодальна. На выбранном отрезке намечаются две пробных точки 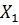 и
и 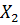
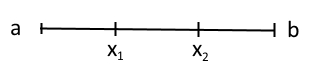
Точки расположены симметрично относительно центра отрезка, их координаты определяются по формуле:
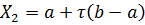 (1)
(1)
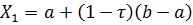 (2)
(2)
Здесь 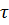 – это отношение отрезка
– это отношение отрезка 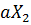 или
или 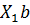 к длине отрезка
к длине отрезка 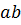 .
.
Алгоритм любого метода исключения отрезков будет следующим:
1. Вычисляются координаты 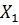 ,
, 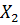 по формулам (1); (2);
по формулам (1); (2);
2. Определяются значения функции 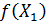 и
и 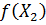
3. Если 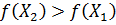 , то исключается отрезок
, то исключается отрезок 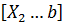 , для этого принимается
, для этого принимается 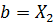 , если
, если 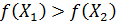 , то исключается отрезок
, то исключается отрезок 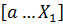 , для этого принимается
, для этого принимается 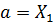 .
.
4. Если 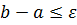 , где
, где 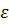 – заданная точность расчета, то в качестве оптимального значения X принимается
– заданная точность расчета, то в качестве оптимального значения X принимается 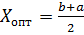 и вычисляется
и вычисляется 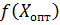 , на этом расчёт заканчивается. Если
, на этом расчёт заканчивается. Если 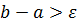 , то возвращаемся к пункту 1.
, то возвращаемся к пункту 1.
Метод золотого сечения соответствует тому же алгоритму, но число 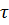 принимается таким, чтобы одна из пробных точек старого отрезка стала пробной точкой нового отрезка.
принимается таким, чтобы одна из пробных точек старого отрезка стала пробной точкой нового отрезка.
Найдём величину 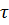 , соответсвующую этому условию. Для этого рассмотрим единичный отрезок, то есть: а=0; b=1;
, соответсвующую этому условию. Для этого рассмотрим единичный отрезок, то есть: а=0; b=1; 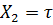 ;
; 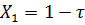 ; Предположим, что отбрасывается правая часть отрезка, тогда должно быть одинаковым отношение длин
; Предположим, что отбрасывается правая часть отрезка, тогда должно быть одинаковым отношение длин
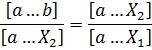
Поэтому:
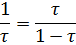
Отсюда получаем квадратное уравнение:
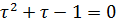
Тогда 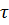 определим как положительный корень этого уравнения:
определим как положительный корень этого уравнения:
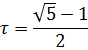
Пусть имеется целевая функция 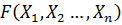 , при этом на оптимизируемые переменные наложено m – ограничений равенств вида
, при этом на оптимизируемые переменные наложено m – ограничений равенств вида 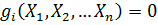 , требуется найти минимум функции F с учётом этих ограничений. Если n=m, то совокупность технических ограничений даёт однозначный набор значений переменных и оптимизация не возможно.
, требуется найти минимум функции F с учётом этих ограничений. Если n=m, то совокупность технических ограничений даёт однозначный набор значений переменных и оптимизация не возможно.
Оптимизация возможна только при условии 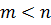 , то величина (n - m) называется числом степеней свободы системы, по смыслу это число переменных, которые могут варьироваться независимо друг от друга.
, то величина (n - m) называется числом степеней свободы системы, по смыслу это число переменных, которые могут варьироваться независимо друг от друга.
Метод Лагранжа состоит в том, что исходная функция F заменяется на так называемую функцию Лагранжа, которая имеет вид
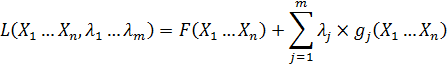
Здесь 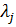 – это вспомогательная переменная, которая называется множителем Лагранжа. Функция L минимизируется классическим методом, то есть составляется и решается следующая система уравнений:
– это вспомогательная переменная, которая называется множителем Лагранжа. Функция L минимизируется классическим методом, то есть составляется и решается следующая система уравнений:
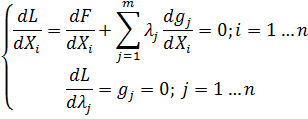
Решая эту систему, находим значения 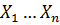 , которые и являются решением задачи оптимизации.
, которые и являются решением задачи оптимизации.
Это не метод оптимизации, а пример использования классической минимизации функции многих переменных.
Пусть имеется некоторая экспериментальная зависимость величины y от x построенная в виде совокупности точек:
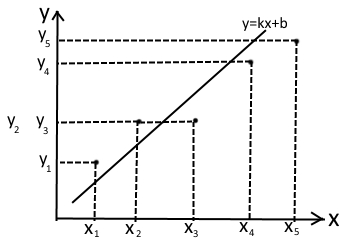
Требуется сгладить эту зависимость, какой либо функцией. Наиболее распространённым методом такого сглаживания является метод наименьших квадратов. Согласно этому методу сумма квадратов отклонений ординат исходных точек от ординат сглаживающих функций должна быть минимальна, то есть если обозначить сглаживающую функцию как y(x), то сумма квадратов будет равна:
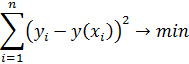
Где n – число точек, 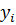 – ординаты точек,
– ординаты точек, 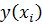 – ординаты сглаживающей функции.
– ординаты сглаживающей функции.
Рассмотрим когда y(x) это линейная функция 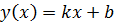 , требуется коэффициенты k и b, целевая функция
, требуется коэффициенты k и b, целевая функция
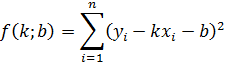
Найдём её минимум классическим методом:
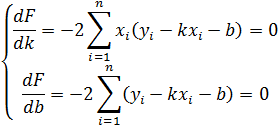
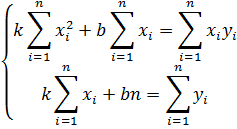
Умножим первое уравнение на m, а второе уравнение на сумму 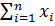
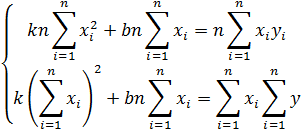
Вычтем второе уравнение из первого:
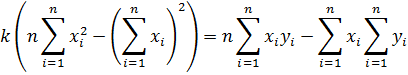
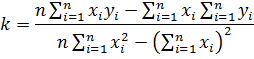
Тогда коэффициент b из второго уравнения:
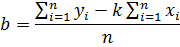
 2015-04-06
2015-04-06 5292
5292
